NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: CirclesExercise 9.4
Class 10 - Mathematics - CHAPTER 9: Circles
Question. 1
If a hexagon ABCDEF circumscribes a circle, prove that
\(AB + CD + EF = BC + DE + FA\).
Answer:
Relation is proved: \(AB + CD + EF = BC + DE + FA\).
Open
Question. 2
Let \(s\) denote the semi-perimeter of a triangle ABC in which \(BC = a\), \(CA = b\), \(AB = c\). If a circle touches the sides BC, CA, AB at D, E, F respectively, prove that \(BD = s - b\).
Answer:
\(BD = s - b\)
Open
Question. 3
From an external point P, two tangents PA and PB are drawn to a circle with centre O. At one point E on the circle, tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD.
Answer:
Perimeter of \(\triangle PCD = 40\,\text{cm}\).
Open
Question. 4
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in Fig. 9.17. Prove that
\(\angle BAT = \angle ACB\).
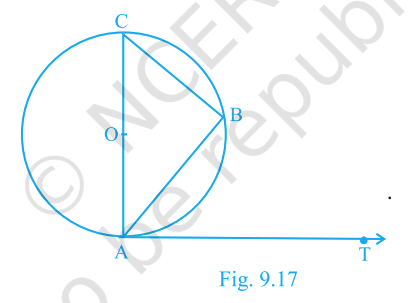
Answer:
\(\angle BAT = \angle ACB\)
Open
Question. 5
Two circles with centres O and O′ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O′P are tangents to the two circles. Find the length of the common chord PQ.
Answer:
Length of chord PQ = 4.8 cm
Open
Question. 6
In a right triangle ABC in which \(\angle B = 90^\circ\), a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
Answer:
The tangent at P bisects BC.
Open
Question. 7
In Fig. 9.18, tangents PQ and PR are drawn to a circle such that \(\angle RPQ = 30^\circ\). A chord RS is drawn parallel to the tangent PQ. Find the \(\angle RQS\).
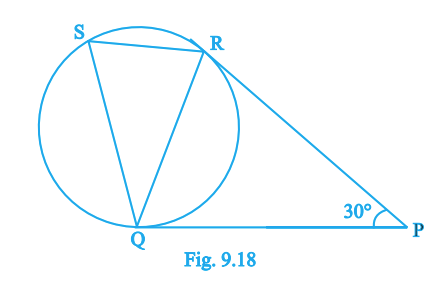
Answer:
\(\angle RQS = 60^\circ\)
Open
Question. 8
AB is a diameter and AC is a chord of a circle with centre O such that \(\angle BAC = 30^\circ\). The tangent at C intersects extended AB at a point D. Prove that \(BC = BD\).
Answer:
\(BC = BD\)
Open
Question. 9
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Answer:
Tangent at mid-point of arc is parallel to chord.
Open
Question. 10
In Fig. 9.19, the common tangent, AB and CD to two circles with centres O and O′ intersect at E. Prove that the points O, E, O′ are collinear.
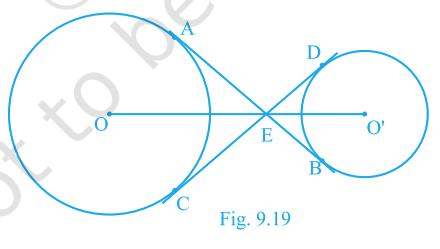
Answer:
O, E, O′ are collinear.
Open
Question. 11
In Fig. 9.20, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.
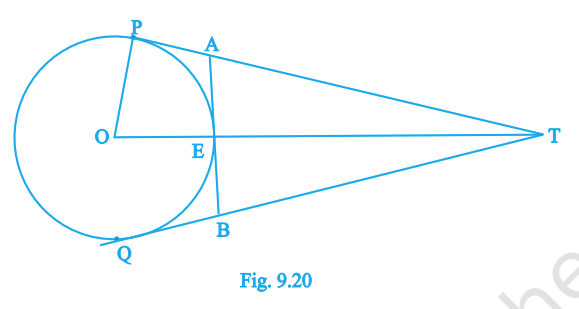
Answer:
\(AB = 12\,\text{cm}\)
Open
Question. 12
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If \(\angle PCA = 110^\circ\), find \(\angle CBA\).
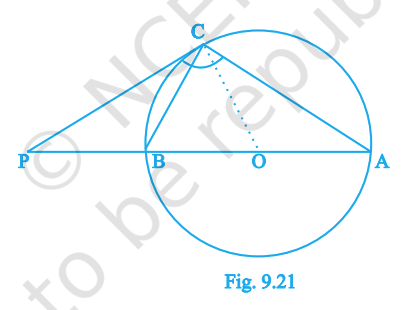
Answer:
\(\angle CBA = 20^\circ\)
Open
Question. 13
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
Answer:
Area = 72 cm²
Open
Question. 14
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the \(\triangle ABC\).
Answer:
Perimeter = 56 cm