NCERT Solutions
Class 10 - Mathematics - Chapter 8: INTRODUCTION TO TRIGONOMETRY - Exercise 8.1Question 2
Class 10 - Mathematics - Chapter 8: INTRODUCTION TO TRIGONOMETRY - Exercise 8.1
Question. 2
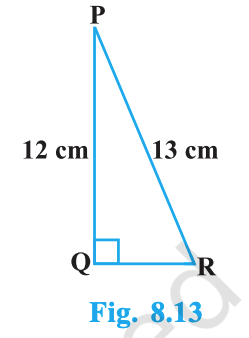
In Fig. 8.13, find tan P − cot R.
Answer:
0
Video Explanation:
Detailed Answer with Explanation:
From Fig. 8.13: \(\triangle PQR\) is right-angled at \(Q\). Given \(PQ = 12\) cm and \(PR = 13\) cm (the slant side).
To find: \(\tan P - \cot R\).
Step 1: Identify the hypotenuse
The hypotenuse is the side opposite the right angle. Since \(\angle Q = 90^\circ\), the hypotenuse is \(PR\). So, \(PR = 13\) cm.
Step 2: Find the third side \(QR\) using Pythagoras theorem
Pythagoras theorem: \(PR^2 = PQ^2 + QR^2\)
Substitute the values:
\(13^2 = 12^2 + QR^2\)
\(169 = 144 + QR^2\)
\(QR^2 = 169 - 144 = 25\)
\(QR = \sqrt{25} = 5\) cm.
Student Note: Here the triangle is a common \(5\text{-}12\text{-}13\) right triangle, so the missing side comes out neatly.
Step 3: Calculate \(\tan P\)
For angle \(P\):
Opposite side = \(QR = 5\) cm, Adjacent side = \(PQ = 12\) cm.
So, \(\tan P = \dfrac{\text{opposite}}{\text{adjacent}} = \dfrac{5}{12}\).
Step 4: Calculate \(\cot R\)
For angle \(R\):
Opposite side = \(PQ = 12\) cm, Adjacent side = \(QR = 5\) cm.
So, \(\cot R = \dfrac{\text{adjacent}}{\text{opposite}} = \dfrac{5}{12}\).
Step 5: Find \(\tan P - \cot R\)
\(\tan P - \cot R = \dfrac{5}{12} - \dfrac{5}{12} = 0\).
Quick Check: In a right triangle, angles \(P\) and \(R\) are complementary, so \(\tan P = \cot R\). That’s why the difference becomes \(0\).