NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.2
Question 3

Question. 3

In Fig. 11.3, a square is inscribed in a circle of diameter \(d\) and another square circumscribes the circle. Is the area of the outer square four times the area of the inner square?

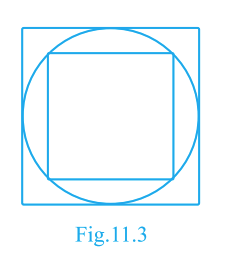
Fig. 11.3 - square in a circle and a square around the circle

Answer:

false

Detailed Answer with Explanation:

Step 1: Let the diameter of the circle be \(d\). Then the radius is half of the diameter:

\(r = \dfrac{d}{2}\).

Step 2: For the inner square (inscribed in the circle):

  • The diagonal of this square is equal to the diameter of the circle (because all 4 vertices touch the circle).
  • So, diagonal of inner square \( = 2r \).
  • If the diagonal of a square is \(d_{sq}\), then side of square = \(\dfrac{d_{sq}}{\sqrt{2}}\).
  • Therefore, side of inner square \(s_i = \dfrac{2r}{\sqrt{2}} = r\sqrt{2}\).
  • Area of inner square \(A_i = (s_i)^2 = (r\sqrt{2})^2 = 2r^2\).

Step 3: For the outer square (circumscribed around the circle):

  • The side of this square is equal to the diameter of the circle, because the circle touches the middle of each side of the square.
  • So, side of outer square \(s_o = 2r\).
  • Area of outer square \(A_o = (s_o)^2 = (2r)^2 = 4r^2\).

Step 4: Compare the two areas:

\(\dfrac{A_o}{A_i} = \dfrac{4r^2}{2r^2} = 2\).

Step 5: The outer square’s area is only 2 times the inner square’s area, not 4 times.

Final Answer: The statement is false.

Open NCERT PDFOpen NCERT Answers PDF