NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4Question 11
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4
Question. 11
The floor of a room is \(5\,\text{m}\times 4\,\text{m}\) and it is covered with circular tiles of diameter 50 cm laid in a rectangular grid as shown. Find the area of the floor that remains uncovered with tiles.
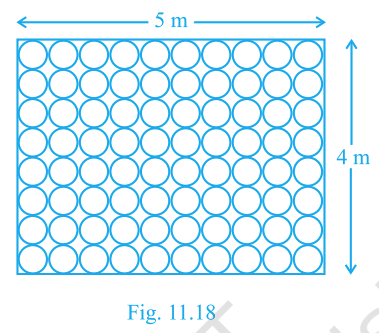
Answer:
\(200000 - 50000\pi\,\text{cm}^2 \;\approx\; 42{,}920\,\text{cm}^2 = 4.292\,\text{m}^2\)
Detailed Answer with Explanation:
Step 1: Convert all dimensions to the same unit.
The floor is given as \(5\,\text{m} \times 4\,\text{m}\). Since the tiles are in cm, convert the floor to cm:
\(5\,\text{m} = 500\,\text{cm}, \; 4\,\text{m} = 400\,\text{cm}.\)
Step 2: Find the area of the floor.
Area of rectangle \(= \text{length} \times \text{breadth}\).
\(500 \times 400 = 200000\,\text{cm}^2.\)
Step 3: Work out how many tiles fit.
Diameter of one tile = 50 cm ⇒ radius = 25 cm.
Along the length: \(500/50 = 10\) tiles fit.
Along the breadth: \(400/50 = 8\) tiles fit.
Total number of tiles = \(10 \times 8 = 80.\)
Step 4: Area of one circular tile.
Area = \(\pi r^2 = \pi (25)^2 = 625\pi\,\text{cm}^2.\)
Step 5: Total area of 80 tiles.
\(80 \times 625\pi = 50000\pi\,\text{cm}^2.\)
Step 6: Uncovered area.
Uncovered area = Floor area – Tile area
= \(200000 - 50000\pi\,\text{cm}^2\).
Step 7: Approximate value.
Take \(\pi \approx 3.1416\).
\(50000\pi \approx 157080.\)
Uncovered area \(= 200000 - 157080 = 42920\,\text{cm}^2.\)
Step 8: Convert back to m² (SI unit).
\(1\,\text{m}^2 = 10000\,\text{cm}^2.\)
So, \(42920\,\text{cm}^2 = 4.292\,\text{m}^2.\)