NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4Question 6
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4
Question. 6
In the trapezium ABCD, \(AB\parallel DC\), \(AB=18\,\text{cm}\), \(DC=32\,\text{cm}\) and the distance between them is \(14\,\text{cm}\). Arcs of equal radii 7 cm with centres A, B, C and D are drawn as in the figure. Find the area of the shaded region.
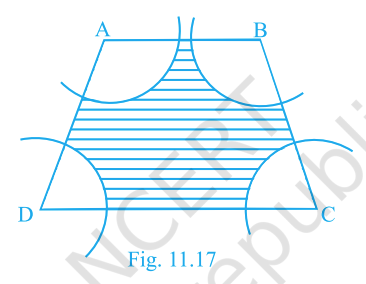
Answer:
\(350 - 49\pi\,\text{cm}^2 \;\approx\; 196.1\,\text{cm}^2\)
Detailed Answer with Explanation:
Step 1: Formula for trapezium area
The area of a trapezium is given by:
\( \text{Area} = \dfrac{1}{2} \times (\text{sum of parallel sides}) \times \text{height} \)
Step 2: Substitute values
Here, \(AB = 18\,\text{cm}\), \(DC = 32\,\text{cm}\), and height = \(14\,\text{cm}\).
So, \( \text{Area} = \dfrac{1}{2} (18 + 32) \times 14 \)
= \( \dfrac{1}{2} (50) \times 14 \)
= \( 25 \times 14 = 350\,\text{cm}^2 \).
Step 3: Find area of circular parts
At each corner A, B, C, D, a quarter-circle is drawn with radius \(7\,\text{cm}\).
Four quarter-circles together make one complete circle.
Area of a circle = \( \pi r^2 \).
Here, \(r = 7\,\text{cm}\).
So, area of the full circle = \( \pi \times 7^2 = 49\pi\,\text{cm}^2 \).
Step 4: Subtract to get shaded area
Shaded region = area of trapezium – area of circle
= \(350 - 49\pi\,\text{cm}^2 \).
Step 5: Approximate value
Take \(\pi \approx 3.14\).
So, \(49\pi \approx 49 \times 3.14 = 153.9\,\text{cm}^2 \).
Therefore, shaded region = \(350 - 153.9 = 196.1\,\text{cm}^2 \).