NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 2: PolynomialsExercise 2.1
Class 10 - Mathematics - CHAPTER 2: Polynomials
Question. 1
If one of the zeroes of the quadratic polynomial \((k-1)x^2 + kx + 1\) is \(-3\), then the value of k is
\(\dfrac{4}{3}\)
\(-\dfrac{4}{3}\)
\(\dfrac{2}{3}\)
\(-\dfrac{2}{3}\)
Open
Question. 2
A quadratic polynomial, whose zeroes are \(-3\) and \(4\), is
\(x^2 - x + 12\)
\(x^2 + x + 12\)
\(\dfrac{x^2}{2} - \dfrac{x}{2} - 6\)
\(2x^2 + 2x - 24\)
Open
Question. 3
If the zeroes of the quadratic polynomial \(x^2 + (a+1)x + b\) are \(2\) and \(-3\), then
\(a = -7,\; b = -1\)
\(a = 5,\; b = -1\)
\(a = 2,\; b = -6\)
\(a = 0,\; b = -6\)
Open
Question. 4
The number of polynomials having zeroes as \(-2\) and \(5\) is
1
2
3
more than 3
Open
Question. 5
Given that one of the zeroes of the cubic polynomial \(ax^3+bx^2+cx+d\) is zero, the product of the other two zeroes is
\(-\dfrac{c}{a}\)
\(\dfrac{c}{a}\)
0
\(-\dfrac{b}{a}\)
Open
Question. 6
If one of the zeroes of the cubic polynomial \(x^3+ax^2+bx+c\) is \(-1\), then the product of the other two zeroes is
\(b-a+1\)
\(b-a-1\)
\(a-b+1\)
\(a-b-1\)
Open
Question. 7
The zeroes of the quadratic polynomial \(x^2 + 99x + 127\) are
both positive
both negative
one positive and one negative
both equal
Open
Question. 8
The zeroes of the quadratic polynomial \(x^2 + kx + k\), where \(k \ne 0\), are:
cannot both be positive
cannot both be negative
are always unequal
are always equal
Open
Question. 9
If the zeroes of the quadratic polynomial \(ax^2 + bx + c\), with \(c \ne 0\), are equal, then
\(c\) and \(a\) have opposite signs
\(c\) and \(b\) have opposite signs
\(c\) and \(a\) have the same sign
\(c\) and \(b\) have the same sign
Open
Question. 10
If one of the zeroes of a quadratic polynomial of the form \(x^2+ax+b\) is the negative of the other, then it
has no linear term and the constant term is negative
has no linear term and the constant term is positive
can have a linear term but the constant term is negative
can have a linear term but the constant term is positive
Open
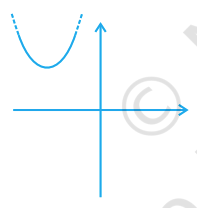
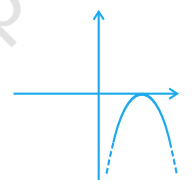
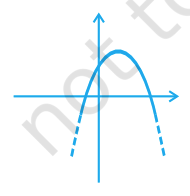
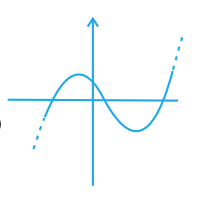
Question. 11
Which of the following is not the graph of a quadratic polynomial?