NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 7: Coordinate GeometryExercise 7.1
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry
Question. 1
The distance of the point \(P(2,3)\) from the x-axis is
2
3
1
5
Handwritten Notes
Open
Question. 2
The distance between the points \(A(0,6)\) and \(B(0,-2)\) is
6
8
4
2
Handwritten Notes
Open
Question. 3
The distance of the point \(P(-6,8)\) from the origin is
8
\(2\sqrt{7}\)
10
6
Handwritten Notes
Open
Question. 4
The distance between the points \((0,5)\) and \((-5,0)\) is
5
\(5\sqrt{2}\)
\(2\sqrt{5}\)
10
Handwritten Notes
Open
Question. 5
AOBC is a rectangle whose three vertices are \(A(0,3),\ O(0,0)\) and \(B(5,0)\). The length of its diagonal is
5
3
\(\sqrt{34}\)
4
Handwritten Notes
Open
Question. 6
The perimeter of a triangle with vertices \((0,4),(0,0),(3,0)\) is
5
12
11
\(7+\sqrt{5}\)
Handwritten Notes
Open
Question. 7
The area of a triangle with vertices \(A(3,0),\ B(7,0)\) and \(C(8,4)\) is
14
28
8
6
Handwritten Notes
Open
Question. 8
The points \((-4,0),(4,0)\) and \((0,3)\) are the vertices of a
right triangle
isosceles triangle
equilateral triangle
scalene triangle
Handwritten Notes
Open
Question. 9
The point which divides the line segment joining \((7,-6)\) and \((3,4)\) in ratio \(1:2\) internally lies in the
I quadrant
II quadrant
III quadrant
IV quadrant
Handwritten Notes
Open
Question. 10
The point which lies on the perpendicular bisector of the line segment joining the points \(A(-2,-5)\) and \(B(2,5)\) is
(0, 0)
(0, 2)
(2, 0)
(-2, 0)
Handwritten Notes
Open
Question. 11
The fourth vertex \(D\) of a parallelogram \(ABCD\) whose three vertices are \(A(-2,3),\ B(6,7)\) and \(C(8,3)\) is
(0, 1)
(0, -1)
(-1, 0)
(1, 0)
Handwritten Notes
Open
Question. 12
If the point \(P(2,1)\) lies on the line segment joining points \(A(4,2)\) and \(B(8,4)\), then
\(AP=\dfrac{1}{3}\,AB\)
\(AP=PB\)
\(PB=\dfrac{1}{3}\,AB\)
\(AP=\dfrac{1}{2}\,AB\)
Handwritten Notes
Open
Question. 13
If \(P\big(\dfrac{a}{3},4\big)\) is the mid-point of the line segment joining the points \(Q(-6,5)\) and \(R(-2,3)\), then the value of \(a\) is
-4
-12
12
-6
Handwritten Notes
Open
Question. 14
The perpendicular bisector of the line segment joining the points \(A(1,5)\) and \(B(4,6)\) cuts the y-axis at
(0, 13)
(0, -13)
(0, 12)
(13, 0)
Handwritten Notes
Open
Question. 15
The coordinates of the point which is equidistant from the three vertices of \(\triangle AOB\) as shown in Fig. 7.1 is
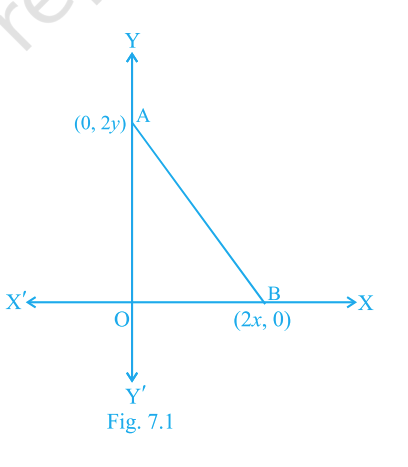
(x, y)
(y, x)
\(\big(\dfrac{x}{2},\dfrac{y}{2}\big)\)
\(\big(\dfrac{y}{2},\dfrac{x}{2}\big)\)
Handwritten Notes
Open
Question. 16
A circle drawn with origin as the centre passes through \(\big(\dfrac{13}{2},0\big)\). The point which does not lie in the interior of the circle is
\(\big(-\dfrac{3}{4},1\big)\)
\(\big(2,\dfrac{7}{3}\big)\)
\(\big(5,-\dfrac{1}{2}\big)\)
\(\big(-6,\dfrac{5}{2}\big)\)
Handwritten Notes
Open
Question. 17
A line intersects the y-axis and x-axis at the points \(P\) and \(Q\), respectively. If \((2,-5)\) is the mid-point of \(PQ\), then the coordinates of \(P\) and \(Q\) are, respectively
(0, -5) and (2, 0)
(0, 10) and (-4, 0)
(0, 4) and (-10, 0)
(0, -10) and (4, 0)
Handwritten Notes
Open
Question. 18
The area of a triangle with vertices \((a,b+c)\), \((b,c+a)\) and \((c,a+b)\) is
\((a+b+c)^2\)
0
\(a+b+c\)
\(abc\)
Handwritten Notes
Open
Question. 19
If the distance between the points \((4,p)\) and \((1,0)\) is 5, then the value of \(p\) is
4 only
\(\pm 4\)
-4 only
0
Handwritten Notes
Open
Question. 20
If the points \(A(1,2)\), \(O(0,0)\) and \(C(a,b)\) are collinear, then
\(a=b\)
\(a=2b\)
\(2a=b\)
\(a=-b\)