NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry

Exercise 7.4

If \((-4,\,3)\) and \((4,\,3)\) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.

\(A(6,1),\ B(8,2)\) and \(C(9,4)\) are three vertices of a parallelogram \(ABCD\). If \(E\) is the midpoint of \(DC\), find the area of \(\triangle ADE\).

The points \(A(x_1,y_1),\ B(x_2,y_2)\) and \(C(x_3,y_3)\) are the vertices of \(\triangle ABC\).

(i) The median from \(A\) meets \(BC\) at \(D\). Find \(D\).

(ii) Find the point \(P\) on \(AD\) such that \(AP:PD=2:1\).

(iii) Find points \(Q\) and \(R\) on medians \(BE\) and \(CF\) respectively such that \(BQ:QE=2:1\) and \(CR:RF=2:1\).

(iv) Hence, write the coordinates of the centroid of \(\triangle ABC\).

The points \(A(1,-2),\ B(2,3),\ C(a,2)\) and \(D(-4,-3)\) form a parallelogram. Find \(a\) and the height of the parallelogram taking \(AB\) as the base.

Students stand on a grid for drill. Points \(A, B, C, D\) are shown below. Is it possible to place Jaspal so that he is equidistant from all four? If yes, give his position.

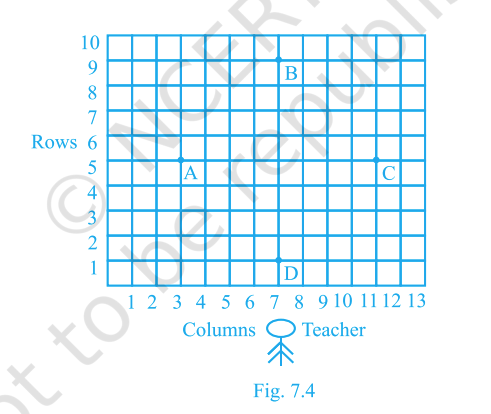
(Use grid coordinates: \(A(3,5),\ B(6,8),\ C(10,5),\ D(7,1)\).)

Ayush travels House \(\to\) Bank \(\to\) School \(\to\) Office along straight segments instead of going directly House \(\to\) Office. If \(H(2,4),\ B(5,8),\ S(13,14),\ O(13,26)\), find the extra distance travelled.