NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4Question 7
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4
Question. 7
In Fig. 9.18, tangents PQ and PR are drawn to a circle such that \(\angle RPQ = 30^\circ\). A chord RS is drawn parallel to the tangent PQ. Find the \(\angle RQS\).
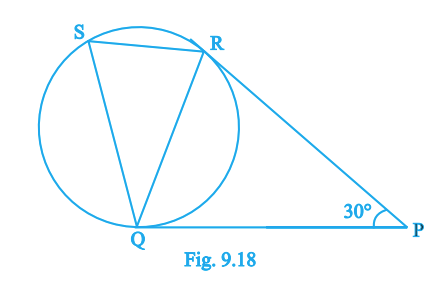
Answer:
\(\angle RQS = 60^\circ\)
Detailed Answer with Explanation:
Step 1: We are given two tangents PQ and PR from point P. The angle between them is \(\angle RPQ = 30^\circ\).
Step 2: In geometry, the angle between two tangents drawn from an external point is related to the angle made at the center by the line joining the points of contact. But here, instead of the center, we are asked about a chord parallel to a tangent.
Step 3: Notice that RS is drawn parallel to the tangent PQ. So, the chord RS and line PQ are parallel.
Step 4: By the alternate segment theorem: The angle between a tangent and a chord through the point of contact is equal to the angle in the opposite segment of the circle.
Step 5: At point R, the tangent PR makes an angle of \(30^\circ\) with PQ. So, inside the circle, the angle subtended by chord RS at point Q will be: \[ \angle RQS = 90^\circ - \angle RPQ \]
Step 6: Substitute the value: \[ \angle RQS = 90^\circ - 30^\circ = 60^\circ \]
Final Answer: Therefore, \(\angle RQS = 60^\circ\).