NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 11
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 11
In Fig. 11.10 (square of side 12 cm), arcs with centres at \(A,B,C,D\) and radius 6 cm pass through the midpoints of adjacent sides, forming a central shaded region. Find the shaded area (use \(\pi=3.14\)).
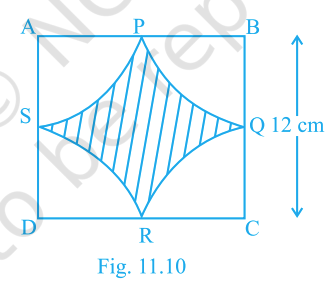
Answer:
\(144 - 36\pi\;\text{cm}^2\;\approx 30.96\,\text{cm}^2\)
Detailed Answer with Explanation:
Step 1: The side of the square is given as 12 cm. Area of a square = (side × side) = \(12 \times 12 = 144\,\text{cm}^2\).
Step 2: At each corner (A, B, C, D), an arc is drawn with radius 6 cm. Each of these arcs is a quarter of a circle (90° part of a circle).
Step 3: There are 4 corners. So, the 4 quarter-circles together make 1 complete circle of radius 6 cm.
Step 4: Area of a circle = \(\pi r^2\). Here, \(r = 6\,\text{cm}\). So, area of the circle = \(3.14 \times 6^2 = 3.14 \times 36 = 113.04\,\text{cm}^2\). (This is the same as \(36\pi\,\text{cm}^2\)).
Step 5: The shaded central region = area of square − area of circle. = \(144 - 113.04 = 30.96\,\text{cm}^2\).
Final Answer: The shaded area is \(144 - 36\pi\,\text{cm}^2 \approx 30.96\,\text{cm}^2\).