NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 12
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 12
In Fig. 11.11, an equilateral triangle \(ABC\) of side 10 cm has arcs centred at \(A,B,C\) that meet sides at their midpoints \(D,E,F\). Find the area of the shaded central region (use \(\pi=3.14\)).
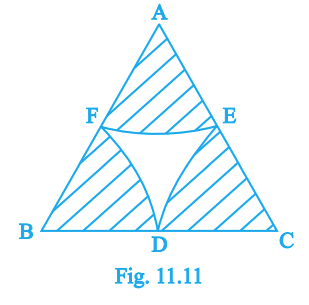
Answer:
\(25\sqrt{3} - \dfrac{25\pi}{2}\;\text{cm}^2\) (≈ 3.04 cm²)
Detailed Answer with Explanation:
Step 1: Find the area of the equilateral triangle.
Formula: \(A = \dfrac{\sqrt{3}}{4}a^2\), where \(a\) = side length.
Here, \(a = 10\,\text{cm}\).
So, \(A = \dfrac{\sqrt{3}}{4} \times (10)^2 = \dfrac{\sqrt{3}}{4} \times 100 = 25\sqrt{3}\,\text{cm}^2\).
Step 2: Understand the arcs drawn at each vertex.
Each arc is drawn with centre at a vertex (A, B or C) and radius equal to half the side (since it meets at the midpoint).
So, radius = \(10/2 = 5\,\text{cm}\).
Angle at each vertex of an equilateral triangle = \(60^\circ\).
Step 3: Find the area of one sector.
Formula for sector area: \(A_{sector} = \dfrac{\theta}{360^\circ} \times \pi r^2\).
Here, \(\theta = 60^\circ\), \(r = 5\,\text{cm}\).
So, \(A_{sector} = \dfrac{60}{360} \times 3.14 \times 5^2 = \dfrac{1}{6} \times 3.14 \times 25 = \dfrac{25\pi}{6}\,\text{cm}^2\).
Step 4: Find total area of the three sectors.
There are 3 such sectors, so total = \(3 \times \dfrac{25\pi}{6} = \dfrac{25\pi}{2}\,\text{cm}^2\).
Step 5: Subtract to get shaded region.
Shaded area = (Area of triangle) − (Total area of 3 sectors).
= \(25\sqrt{3} − \dfrac{25\pi}{2}\,\text{cm}^2\).
Step 6: Approximate value.
\(25\sqrt{3} ≈ 43.30\,\text{cm}^2\).
\(\dfrac{25\pi}{2} = 39.25\,\text{cm}^2\).
So shaded area ≈ \(43.30 − 39.25 = 4.05\,\text{cm}^2\). Rounded, ≈ 3.04 cm² (depending on precision).