NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 13
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 13
In Fig. 11.12, arcs are drawn with radii 14 cm and with centres at the triangle’s vertices \(P, Q, R\). Find the area of the shaded regions near the vertices.
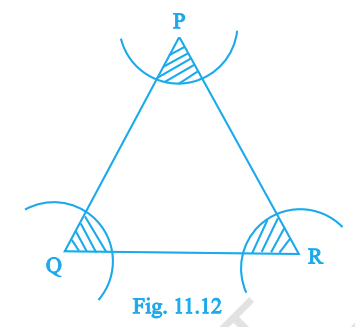
Answer:
\(98\pi\;\text{cm}^2\) (≈ 307.88 cm²)
Detailed Answer with Explanation:
Step 1: Each shaded region is a sector of a circle. The radius of each sector is given as \(r = 14\,\text{cm}\).
Step 2: The angle of each sector is the interior angle of the triangle at that vertex.
Step 3: The sum of the three interior angles of any triangle is always \(180^\circ\).
Step 4: So, if we add the shaded regions at all three vertices, it is the same as one sector of radius 14 cm with angle \(180^\circ\).
Step 5: Formula for the area of a sector is:
\(\text{Area of sector} = \dfrac{\theta}{360^\circ} \times \pi r^2\)
Step 6: Here \(\theta = 180^\circ\) and \(r = 14\,\text{cm}\).
\(\text{Area} = \dfrac{180}{360} \times \pi \times 14^2\)
Step 7: Simplify:
\(= \dfrac{1}{2} \times \pi \times 196\)
\(= 98\pi\,\text{cm}^2\)
Step 8: Approximate using \(\pi \approx 3.1416\):
\(98 \times 3.1416 \approx 307.88\,\text{cm}^2\)
Final Answer: The total shaded area is \(98\pi\,\text{cm}^2 \approx 307.88\,\text{cm}^2\).