NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 6
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 6
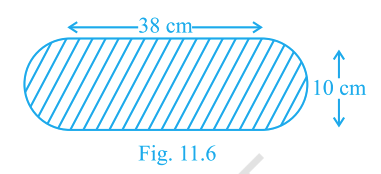
Find the area of the flower bed with semicircular ends shown in Fig. 11.6. The overall length is 38 cm and the overall width is 10 cm.
Answer:
\(280 + 25\pi\;\text{cm}^2\) (≈ 358.50 cm²)
Detailed Answer with Explanation:
Step 1: Identify the shape
The figure looks like a rectangle in the middle with two semicircles (half-circles) attached at the two ends. Together, the two semicircles make one complete circle.
Step 2: Note the given measurements
- Overall length = 38 cm
- Overall width (also the diameter of semicircle) = 10 cm
Step 3: Find the radius of the semicircle
Radius = Diameter ÷ 2 = 10 ÷ 2 = 5 cm.
Step 4: Find the length of the rectangular part
The full length = 38 cm. But at both ends we have semicircles of radius 5 cm each, so total semicircle length = 2 × 5 = 10 cm. Rectangular part length = 38 – 10 = 28 cm.
Step 5: Calculate the area of the rectangle
Area = Length × Breadth = 28 × 10 = 280 cm².
Step 6: Calculate the area of the circle formed by the two semicircles
Area of circle = πr² = π × 5² = 25π cm².
Step 7: Add both areas
Total Area = Rectangle area + Circle area = 280 + 25π cm².
Step 8: Approximate value
If we take π ≈ 3.14, 25π ≈ 25 × 3.14 = 78.5. So total area ≈ 280 + 78.5 = 358.5 cm².
Final Answer: 280 + 25π cm² (≈ 358.5 cm²)