NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 7
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 7
In Fig. 11.7, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (use \(\pi = 3.14\)).
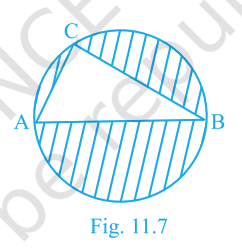
Answer:
54.5 cm²
Detailed Answer with Explanation:
Step 1: Look at the figure. AB is the diameter of the circle. Point C lies on the circle. By Thales' theorem, if a triangle is drawn using the diameter as one side, the angle at the opposite vertex is a right angle (90°). So, \(\triangle ACB\) is a right-angled triangle at C.
Step 2: In this right triangle, we are given AC = 6 cm and BC = 8 cm. To find AB (the diameter), we use the Pythagoras theorem:
\(AB = \sqrt{AC^2 + BC^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\,\text{cm}\).
Step 3: Radius of the circle = half of the diameter = \(\tfrac{10}{2} = 5\,\text{cm}\).
Step 4: Area of the circle is given by formula \(A = \pi r^2\). Substituting values:
\(A = 3.14 \times 5^2 = 3.14 \times 25 = 78.5\,\text{cm}^2\).
Step 5: Area of triangle \(ABC\): formula is \(\tfrac{1}{2} \times \text{base} \times \text{height}\). Here base = 6 cm, height = 8 cm:
\(A = \tfrac{1}{2} \times 6 \times 8 = 24\,\text{cm}^2\).
Step 6: Shaded region = Area of circle − Area of triangle.
= \(78.5 − 24 = 54.5\,\text{cm}^2\).
Final Answer: The area of the shaded region is 54.5 cm².