NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 8
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 8
Find the area of the shaded field shown in Fig. 11.8. (Top width 8 m, left height 6 m with a semicircular bulge, right height 4 m with a semicircular bulge.)
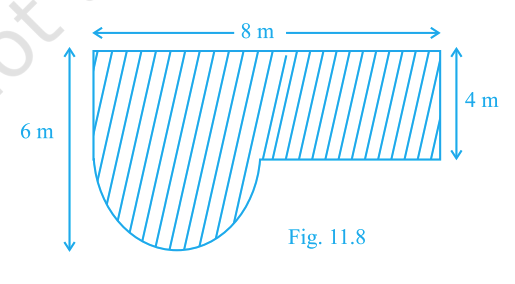
Answer:
\(32 + 6.5\pi\;\text{m}^2\) (≈ 52.42 m²)
Detailed Answer with Explanation:
Step 1: Observe the figure.
The field has three parts:
- A rectangle in the middle (length = 8 m, height = 4 m).
- A semicircle on the left side with radius 3 m (because height = 6 m ⇒ diameter = 6 m ⇒ radius = 3 m).
- A semicircle on the right side with radius 2 m (because height = 4 m ⇒ diameter = 4 m ⇒ radius = 2 m).
Step 2: Find the area of the rectangle.
Area of rectangle = length × breadth
= 8 m × 4 m = 32 m².
Step 3: Find the area of the right semicircle.
Formula for area of a semicircle = (1/2) × π × r²
Here radius r = 2 m.
So, area = (1/2) × π × (2 m)²
= (1/2) × π × 4 m²
= 2π m².
Step 4: Find the area of the left semicircle.
Radius r = 3 m (since diameter = 6 m).
Area = (1/2) × π × (3 m)²
= (1/2) × π × 9 m²
= 4.5π m².
Step 5: Add all areas.
Total area = Rectangle + Right semicircle + Left semicircle
= 32 m² + 2π m² + 4.5π m²
= 32 m² + 6.5π m².
Step 6: Approximate value using π = 3.1416.
= 32 + 6.5 × 3.1416
= 32 + 20.42
= 52.42 m² (approx).
Final Answer: The area of the shaded field is \(32 + 6.5\pi\;\text{m}^2\) ≈ 52.42 m².