NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 9
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 9
Find the area of the shaded region in Fig. 11.9 (outer rectangle 26 m × 12 m; inner 'stadium' has total length 20 m and width 4 m).
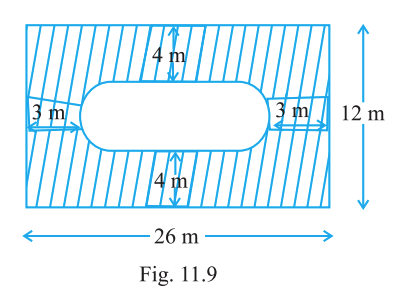
Answer:
\(248 - 4\pi\;\text{m}^2\) (≈ 235.43 m²)
Detailed Answer with Explanation:
Step 1: Find area of the outer rectangle
Length = 26 m, Width = 12 m
Area = length × width = \(26 \times 12 = 312\,\text{m}^2\)
Step 2: Understand the inner shape
The inner figure is like a small "stadium".
- Its total length = 20 m
- Its width = 4 m
This shape is made up of:
- a rectangle in the middle
- and two semicircles (together making one full circle) at the ends
Step 3: Radius of the semicircles
Width = 4 m, so diameter = 4 m
Radius = diameter ÷ 2 = \(4 \div 2 = 2\,\text{m}\)
Step 4: Length of the rectangle part inside
Total length = 20 m
But at both ends, circles take up \(2r = 4\,\text{m}\).
So rectangle length = total length − 2r = \(20 − 4 = 16\,\text{m}\)
Step 5: Area of the inner stadium shape
- Rectangle area = length × width = \(16 \times 4 = 64\,\text{m}^2\)
- Circle area = \(\pi r^2 = \pi \times 2^2 = 4\pi\,\text{m}^2\)
Total inner area = rectangle + circle = \(64 + 4\pi\,\text{m}^2\)
Step 6: Area of shaded region
Shaded = Outer rectangle − Inner shape
= \(312 − (64 + 4\pi) = 248 − 4\pi\,\text{m}^2\)
Step 7: Approximate value
Take \(\pi = 3.1416\)
\(248 − 4\pi = 248 − 12.5664 ≈ 235.43\,\text{m}^2\)