NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4Question 17
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.4
Question. 17
Find the area of the shaded region shown in Fig. 11.20.
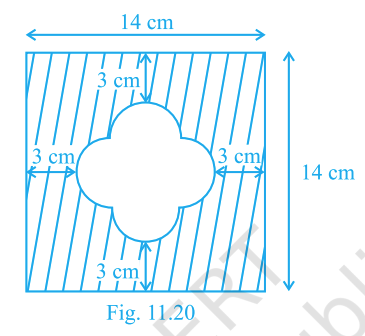
Answer:
\(196 - 18\pi\,\text{cm}^2 \;\approx\; 139.5\,\text{cm}^2\)
Detailed Answer with Explanation:
Step 1: The outer shape is a square of side \(14\,\text{cm}\).
Area of square = side × side = \(14 \times 14 = 196\,\text{cm}^2\).
Step 2: Inside the square, there is a flower-like figure made by 4 semicircles.
Each semicircle has radius \(3\,\text{cm}\).
Step 3: Area of one semicircle = \(\tfrac{1}{2} \pi r^2\).
= \(\tfrac{1}{2} \pi (3^2) = \tfrac{1}{2} \pi \times 9 = 4.5\pi\,\text{cm}^2\).
Step 4: There are 4 such semicircles.
Total area of 4 semicircles = \(4 \times 4.5\pi = 18\pi\,\text{cm}^2\).
Step 5: The shaded region is the square area minus the 4 semicircles area.
Shaded area = \(196 - 18\pi\,\text{cm}^2\).
Step 6: Approximating \(\pi \approx 3.14\):
\(18 \pi = 18 \times 3.14 = 56.52\,\text{cm}^2\).
Shaded area = \(196 - 56.52 = 139.48 \approx 139.5\,\text{cm}^2\).
Final Answer: \(\mathbf{139.5\,\text{cm}^2}\)