NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 12: Surface Areas & Volumes - Exercise 12.3Question 8
Class 10 - Mathematics - CHAPTER 12: Surface Areas & Volumes - Exercise 12.3
Question. 8
Two solid cones \(A\) and \(B\) are placed in a cylindrical tube as shown.
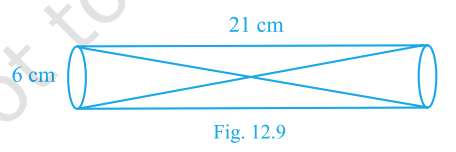
The ratio of their capacities is \(2:1\). Find the heights and capacities of the cones. Also find the volume of the remaining portion of the cylinder (tube length 21 cm, inner diameter 6 cm).
Answer:
Heights: \(14\,\text{cm}\) and \(7\,\text{cm}\).
Capacities: \(42\pi\,\text{cm}^3\) and \(21\pi\,\text{cm}^3\).
Remaining cylinder volume: \(126\pi\,\text{cm}^3\).
Detailed Answer with Explanation:
Step 1: The cylindrical tube has an inner diameter of \(6\,\text{cm}\). Therefore, the radius of the cylinder (and also of both cones) is: \(r = \dfrac{6}{2} = 3\,\text{cm}\).
Step 2: The length (or height) of the tube is given as \(21\,\text{cm}\). The two cones are placed one above the other inside the tube. So, the sum of their heights must be: \(h_A + h_B = 21\,\text{cm}\).
Step 3: The capacity (volume) of a cone is proportional to its height if the radius is the same. Formula: \(V = \tfrac{1}{3}\pi r^2 h\). Here, both cones have the same base radius (\(3\,\text{cm}\)), so the ratio of their volumes is the same as the ratio of their heights. Given: volume ratio \(= 2:1\). So, \(h_A : h_B = 2:1\).
Step 4: Let \(h_A = 2x\) and \(h_B = x\). Then, \(2x + x = 21 \Rightarrow 3x = 21 \Rightarrow x = 7\). Therefore: \(h_A = 14\,\text{cm}, h_B = 7\,\text{cm}\).
Step 5: Find the volumes of the cones using the formula \(V = \tfrac{1}{3}\pi r^2 h\).
- For cone A: \(V_A = \tfrac{1}{3} \pi (3^2)(14) = \tfrac{1}{3}\pi \times 9 \times 14 = 42\pi\,\text{cm}^3\).
- For cone B: \(V_B = \tfrac{1}{3} \pi (3^2)(7) = \tfrac{1}{3}\pi \times 9 \times 7 = 21\pi\,\text{cm}^3\).
Step 6: Find the volume of the entire cylinder. Formula: \(V = \pi r^2 h\). \(V_{cylinder} = \pi (3^2)(21) = \pi \times 9 \times 21 = 189\pi\,\text{cm}^3\).
Step 7: The remaining portion of the cylinder is the cylinder volume minus the volumes of the two cones. \(V_{remaining} = 189\pi - (42\pi + 21\pi) = 189\pi - 63\pi = 126\pi\,\text{cm}^3\).
Final Answer: Heights of the cones: \(14\,\text{cm}\) and \(7\,\text{cm}\). Capacities: \(42\pi\,\text{cm}^3\) and \(21\pi\,\text{cm}^3\). Remaining volume of cylinder: \(126\pi\,\text{cm}^3\).