NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 12: Surface Areas & Volumes - Exercise 12.3Question 9
Class 10 - Mathematics - CHAPTER 12: Surface Areas & Volumes - Exercise 12.3
Question. 9
An ice-cream cone with hemispherical top has radius 5 cm and height 10 cm (see figure).
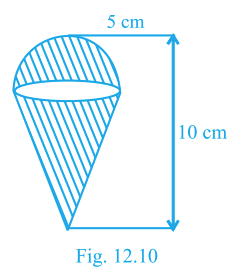
Calculate the volume of ice cream, if \(\dfrac16\) of the cone part is left unfilled.
Answer:
\(\displaystyle \dfrac{1375}{9}\pi\;\text{cm}^3\;\approx 4.80\times10^2\,\text{cm}^3\)
Detailed Answer with Explanation:
Step 1: Identify the shape of the ice cream.
- The ice cream has two parts:
- A hemisphere on the top.
- A cone at the bottom.
- Radius of both = \(r = 5\,\text{cm}\).
- Height of cone = \(h = 10\,\text{cm}\).
Step 2: Volume of the hemisphere.
Formula for volume of hemisphere = \(\dfrac{2}{3}\pi r^3\).
Substitute values: \(\dfrac{2}{3}\pi (5^3) = \dfrac{2}{3}\pi (125) = \dfrac{250}{3}\pi\,\text{cm}^3\).
Step 3: Volume of the full cone.
Formula for volume of cone = \(\dfrac{1}{3}\pi r^2 h\).
Substitute values: \(\dfrac{1}{3}\pi (5^2)(10) = \dfrac{1}{3}\pi (25)(10) = \dfrac{250}{3}\pi\,\text{cm}^3\).
Step 4: Only \(\tfrac{5}{6}\) of the cone is filled.
So, filled cone volume = \(\dfrac{5}{6} \times \dfrac{250}{3}\pi = \dfrac{625}{9}\pi\,\text{cm}^3\).
Step 5: Total volume of ice cream.
Add hemisphere volume and filled cone volume:
\(\dfrac{250}{3}\pi + \dfrac{625}{9}\pi = \dfrac{750}{9}\pi + \dfrac{625}{9}\pi = \dfrac{1375}{9}\pi\,\text{cm}^3\).
Step 6: Approximate numerical value.
\(\dfrac{1375}{9}\pi \approx 480\,\text{cm}^3\).
Final Answer: The volume of the ice cream is about \(480\,\text{cm}^3\).