NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 2: Polynomials - Exercise 2.1Question 11
Class 10 - Mathematics - CHAPTER 2: Polynomials - Exercise 2.1
Question. 11
Which of the following is not the graph of a quadratic polynomial?
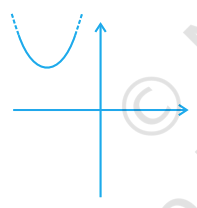
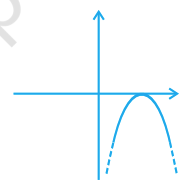
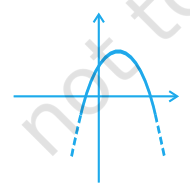
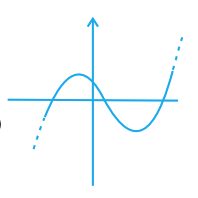
Detailed Answer with Explanation:
Step 1: Recall the property of quadratic graphs.
The graph of a quadratic polynomial \(ax^2 + bx + c\) is always a parabola.
A parabola is a smooth U-shaped curve that opens either upwards (if \(a > 0\)) or downwards (if \(a < 0\)).
Important: A quadratic polynomial graph can have only one turning point, called its vertex.
Step 2: Check each option.
Option (A): The graph is a parabola opening upwards. Valid quadratic graph.
Option (B): The graph is a parabola opening downwards. Valid quadratic graph.
Option (C): The graph is also a parabola opening downwards. Valid quadratic graph.
Option (D): The curve bends twice, showing two turning points. ❌ This is not possible for a quadratic polynomial, but it is possible for a cubic polynomial.
Conclusion: The graph in option (D) is not the graph of a quadratic polynomial.
Correct answer: (D).