NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: TrianglesExercise 6.1
Class 10 - Mathematics - CHAPTER 6: Triangles
Question. 1
1. In Fig. 6.2, \(\angle BAC = 90^\circ\) and \(AD \perp BC\). Then,
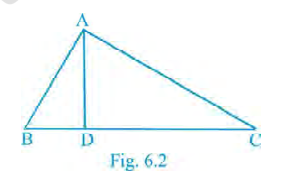
\(BD\cdot CD = BC^2\)
\(AB\cdot AC = BC^2\)
\(BD\cdot CD = AD^2\)
\(AB\cdot AC = AD^2\)
Open
Question. 2
2. The diagonals of a rhombus are 16 cm and 12 cm. The side length is
9 cm
10 cm
8 cm
20 cm
Open
Question. 3
3. If \(\triangle ABC \sim \triangle EDF\) and \(\triangle ABC\) is not similar to \(\triangle DEF\), which is not true?
\(BC\cdot EF = AC\cdot FD\)
\(AB\cdot EF = AC\cdot DE\)
\(BC\cdot DE = AB\cdot EF\)
\(BC\cdot DE = AB\cdot FD\)
Open
Question. 4
4. If in triangles \(ABC\) and \(PQR\),
\(\dfrac{AB}{QR} = \dfrac{BC}{PR} = \dfrac{CA}{PQ}\), then
\(\triangle PQR \sim \triangle CAB\)
\(\triangle PQR \sim \triangle ABC\)
\(\triangle CBA \sim \triangle PQR\)
\(\triangle BCA \sim \triangle PQR\)
Open
Question. 5
5. In Fig. 6.3, lines \(AC\) and \(BD\) intersect at \(P\). Given \(PA=6\,\text{cm},\; PB=3\,\text{cm},\; PC=2.5\,\text{cm},\; PD=5\,\text{cm},\; \(\angle APB=50^\circ\) and \(\angle CDP=30^\circ\). Find \(\angle PBA\).
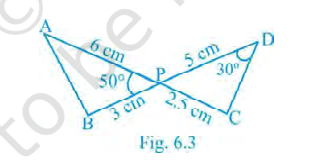
50°
30°
60°
100°
Open
Question. 6
6. In triangles \(DEF\) and \(PQR\), if \(\angle D = \angle Q\) and \(\angle R = \angle E\), which is not true?
\(\dfrac{EF}{PR} = \dfrac{DF}{PQ}\)
\(\dfrac{DE}{PQ} = \dfrac{EF}{RP}\)
\(\dfrac{DE}{QR} = \dfrac{DF}{PQ}\)
\(\dfrac{EF}{RP} = \dfrac{DE}{QR}\)
Open
Question. 7
7. In triangles \(ABC\) and \(DEF\), if \(\angle B=\angle E\), \(\angle F=\angle C\) and \(AB=3\,DE\), the triangles are
congruent but not similar
similar but not congruent
neither
congruent as well as similar
Open
Question. 8
8. Given \(\triangle ABC \sim \triangle PQR\) and \(\dfrac{BC}{QR}=\dfrac{1}{3}\), then \(\dfrac{\operatorname{ar}(PRQ)}{\operatorname{ar}(BCA)}\) equals
9
3
\(\dfrac{1}{3}\)
\(\dfrac{1}{9}\)
Open
Question. 9
9. Given \(\triangle ABC \sim \triangle DFE\) with \(\angle A=30^\circ\), \(\angle C=50^\circ\), \(AB=5\,\text{cm}\), \(AC=8\,\text{cm}\) and \(DF=7.5\,\text{cm}\). Which is true?
\(DE=12\,\text{cm},\; \angle F=50^\circ\)
\(DE=12\,\text{cm},\; \angle F=100^\circ\)
\(EF=12\,\text{cm},\; \angle D=100^\circ\)
\(EF=12\,\text{cm},\; \angle D=30^\circ\)
Open
Question. 10
10. If in triangles \(ABC\) and \(DEF\), \(\dfrac{AB}{DE}=\dfrac{BC}{FD}\), then they will be similar when
\(\angle B=\angle E\)
\(\angle A=\angle D\)
\(\angle B=\angle D\)
\(\angle A=\angle F\)
Open
Question. 11
11. If \(\triangle ABC \sim \triangle QRP\) and \(\dfrac{\operatorname{ar}(ABC)}{\operatorname{ar}(PQR)}=\dfrac{9}{4}\), with \(AB=18\,\text{cm}\) and \(BC=15\,\text{cm}\), then \(PR\) equals
10 cm
12 cm
\(\dfrac{20}{3}\) cm
8 cm
Open
Question. 12
12. If \(S\) is a point on side \(PQ\) of \(\triangle PQR\) such that \(PS=QS=RS\), then
\(PR\cdot QR = RS^2\)
\(QS^2 + RS^2 = QR^2\)
\(PR^2 + QR^2 = PQ^2\)
\(PS^2 + RS^2 = PR^2\)