NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: TrianglesExercise 6.3
Class 10 - Mathematics - CHAPTER 6: Triangles
Question. 1
In \(\triangle PQR\), suppose \(PR^2 - PQ^2 = QR^2\) and \(M\) lies on \(PR\) with \(QM \perp PR\). Prove that \(QM^2 = PM \cdot MR\).
Answer:
Proved.
Open
Question. 2
Find the value of \(x\) for which \(DE \parallel AB\) in Fig. 6.8.
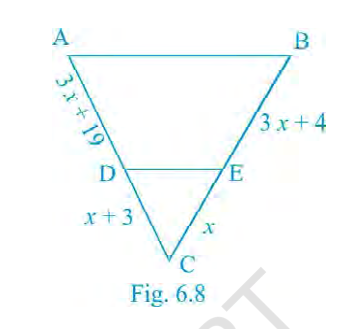
Answer:
\(x=2\)
Open
Question. 3
In Fig. 6.9, if \(\angle 1=\angle 2\) and \(\triangle NSQ \cong \triangle MTR\), prove that \(\triangle PTS \sim \triangle PRQ\).
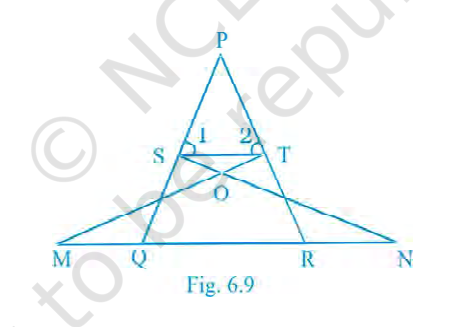
Answer:
Proved.
Open
Question. 4
Diagonals of a trapezium \(PQRS\) intersect at \(O\). If \(PQ\parallel RS\) and \(PQ=3\,RS\), find \(\dfrac{\operatorname{ar}(\triangle POQ)}{\operatorname{ar}(\triangle ROS)}\).
Answer:
\(9:1\)
Open
Question. 5
In Fig. 6.10, if \(AB\parallel DC\) and lines \(AC\) and \(PQ\) meet at \(O\), prove that \(OA\cdot CQ = OC\cdot AP\).
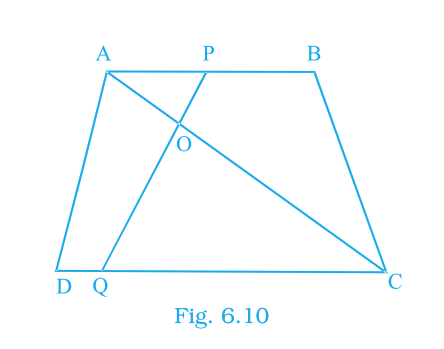
Answer:
Proved.
Open
Question. 6
Find the altitude of an equilateral triangle of side 8 cm.
Answer:
\(4\sqrt{3}\,\text{cm}\)
Open
Question. 7
If \(\triangle ABC \sim \triangle DEF\), with \(AB=4\,\text{cm}\), \(DE=6\,\text{cm}\), \(EF=9\,\text{cm}\) and \(FD=12\,\text{cm}\), find the perimeter of \(\triangle ABC\).
Answer:
18 cm
Open
Question. 8
In Fig. 6.11, if \(DE\parallel BC\), find \(\operatorname{ar}(ADE):\operatorname{ar}(DECB)\).
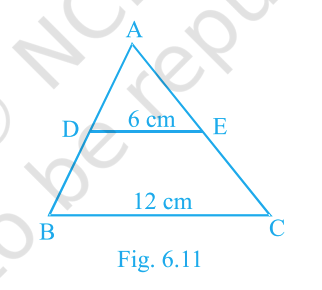
Answer:
\(1:3\)
Open
Question. 9
In trapezium \(ABCD\) with \(AB\parallel DC\), points \(P\) and \(Q\) lie on \(AD\) and \(BC\) respectively, with \(PQ\parallel DC\). If \(PD=18\,\text{cm}\), \(BQ=35\,\text{cm}\) and \(QC=15\,\text{cm}\), find \(AD\).
Answer:
60 cm
Open
Question. 10
Corresponding sides of two similar triangles are in the ratio \(2:3\). If the area of the smaller is \(48\,\text{cm}^2\), find the area of the larger triangle.
Answer:
108 cm²
Open
Question. 11
In \(\triangle PQR\), point \(N\) lies on \(PR\) with \(QN\perp PR\). If \(PN\cdot NR = QN^2\), prove that \(\angle PQR = 90^\circ\).
Answer:
Proved.
Open
Question. 12
Areas of two similar triangles are \(36\,\text{cm}^2\) and \(100\,\text{cm}^2\). If a corresponding side of the larger is 20 cm, find the corresponding side of the smaller.
Answer:
12 cm
Open
Question. 13
In Fig. 6.12, if \(\angle ACB = \angle CDA\), \(AC=8\,\text{cm}\) and \(AD=3\,\text{cm}\), find \(BD\).
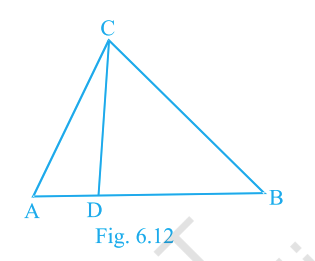
Answer:
\(\dfrac{55}{3}\,\text{cm}\)
Open
Question. 14
A 15 m tower casts a 24 m shadow. At the same time a telephone pole casts a 16 m shadow. Find the pole’s height.
Answer:
10 m
Open
Question. 15
A 10 m ladder leans against a vertical wall with its foot 6 m from the wall. Find the height reached on the wall.
Answer:
8 m