NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: TrianglesExercise 6.2
Class 10 - Mathematics - CHAPTER 6: Triangles
Question. 1
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons.
Answer:
No.
Handwritten Notes
Open
Question. 2
It is given that \(\triangle DEF \sim \triangle RPQ\). Is it true that \(\angle D=\angle R\) and \(\angle F=\angle P\)? Why?
Answer:
No. \(\angle D=\angle R\) is true, but \(\angle F=\angle P\) is false..
Open
Question. 3
Points \(A\) and \(B\) lie on sides \(PQ\) and \(PR\) of \(\triangle PQR\) such that \(PQ=12.5\,\text{cm}\), \(PA=5\,\text{cm}\), \(PB=4\,\text{cm}\) and \(BR=6\,\text{cm}\). Is \(AB\parallel QR\)? Give reasons.
Answer:
Yes.
Open
Question. 4
In Fig. 6.4, \(BD\) and \(CE\) intersect each other at \(P\). Is \(\triangle PBC \sim \triangle PDE\)? Why?
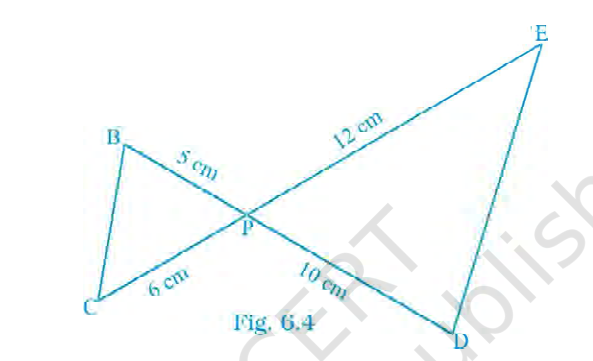
Answer:
Yes.
Open
Question. 5
In triangles \(PQR\) and \(MST\), \(\angle P=55^\circ,\; \angle Q=25^\circ\) and \(\angle M=100^\circ,\; \angle S=25^\circ\). Is \(\triangle QPR \sim \triangle TSM\)? Why?
Answer:
No. But \(\triangle QPR \sim \triangle STM\).
Open
Question. 6
Is the following statement true? Why?
“Two quadrilaterals are similar if their corresponding angles are equal.”
Answer:
False.
Open
Question. 7
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of another triangle. Are the two triangles similar? Why?
Answer:
Yes.
Open
Question. 8
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
Answer:
Yes.
Open
Question. 9
The ratio of the corresponding altitudes of two similar triangles is \(\dfrac{3}{5}\). Is it correct to say that ratio of their areas is \(\dfrac{6}{5}\)? Why?
Answer:
No. The area ratio is \(\left(\dfrac{3}{5}\right)^2=\dfrac{9}{25}\).
Open
Question. 10
Point \(D\) is on side \(QR\) of \(\triangle PQR\) with \(PD\perp QR\). Is \(\triangle PQD \sim \triangle RPD\)? Why?
Answer:
No (not necessarily).
Open
Question. 11
In Fig. 6.5, if \(\angle D = \angle C\), is it true that \(\triangle ADE \sim \triangle ACB\)? Why?
Answer:
Yes.
Open
Question. 12
Is the following statement always true? “If an angle of one triangle equals an angle of another and two sides of one triangle are proportional to the corresponding two sides of the other triangle, then the triangles are similar.” Give reasons.
Answer:
Not always.