NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles

Exercise 6.4

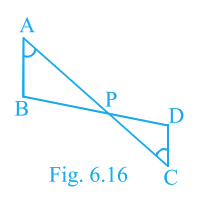
In Fig. 6.16, if \(\angle A = \angle C\), \(AB = 6\,\text{cm}\), \(BP = 15\,\text{cm}\), \(AP = 12\,\text{cm}\) and \(CP = 4\,\text{cm}\), find the lengths \(PD\) and \(CD\).

Given \(\triangle ABC \sim \triangle EDF\) with \(AB=5\,\text{cm}\), \(AC=7\,\text{cm}\), \(DE=12\,\text{cm}\), \(DF=15\,\text{cm}\). Find the remaining sides.

Prove: If a line is drawn parallel to one side of a triangle to meet the other two sides, then it divides those sides in the same ratio.

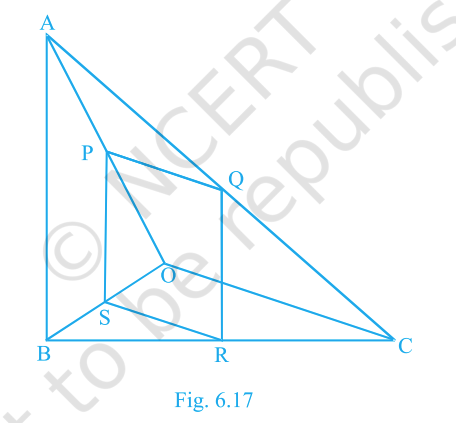
In Fig. 6.17, \(PQRS\) is a parallelogram and \(AB\parallel PS\). Prove that \(OC\parallel SR\).

A 5 m ladder reaches a wall at height 4 m. If the foot is moved \(1.6\,\text{m}\) towards the wall, by how much does the top slide up?

City route: \(AC\perp CB\), \(AC=2x\) km, \(CB=2(x+7)\) km. A direct highway \(AB=26\) km is planned. How many km are saved?

A flag pole 18 m high casts a 9.6 m shadow. Find the distance from the top of the pole to the far end of the shadow.

A lamp is on a 6 m pole. A 1.5 m woman casts a 3 m shadow. How far is she from the pole?

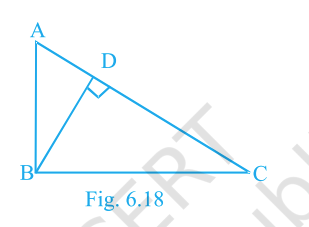
In Fig. 6.18, \(\triangle ABC\) is right-angled at \(B\) and \(BD\perp AC\). If \(AD=4\,\text{cm}\) and \(CD=5\,\text{cm}\), find \(BD\) and \(AB\).

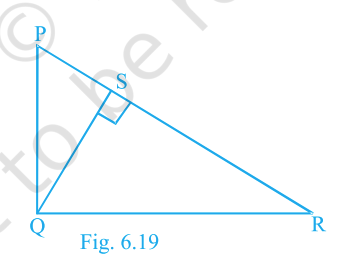
In Fig. 6.19, \(\triangle PQR\) is right-angled at \(Q\) and \(QS\perp PR\). If \(PQ=6\,\text{cm}\), \(PS=4\,\text{cm}\), find \(QS\), \(RS\) and \(QR\).

In \(\triangle PQR\), let \(PD\perp QR\) with \(D\in QR\). If \(PQ=a\), \(PR=b\), \(QD=c\) and \(DR=d\), prove

\[(a+b)(a-b)=(c+d)(c-d).\]

In a quadrilateral \(ABCD\), \(\angle A+\angle D=90^\circ\). Prove that

\[AC^2+BD^2=AD^2+BC^2.\]

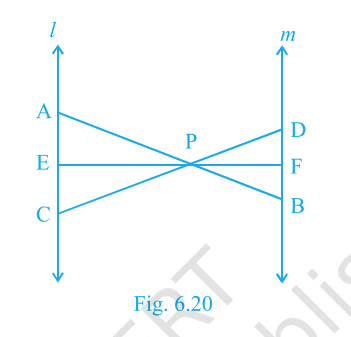
In Fig. 6.20, \(\ell\parallel m\) and the segments \(AB,\,CD,\,EF\) meet at \(P\). Prove

\[\dfrac{AE}{BF}=\dfrac{AC}{BD}=\dfrac{CE}{FD}.\]

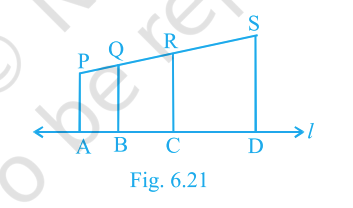
In Fig. 6.21, \(PA, QB, RC, SD\) are all perpendicular to a line \(\ell\). Given \(AB=6\,\text{cm}\), \(BC=9\,\text{cm}\), \(CD=12\,\text{cm}\) and \(SP=36\,\text{cm}\). Find \(PQ, QR, RS\).

In a trapezium \(ABCD\) with \(AB\parallel DC\), diagonals \(AC\) and \(BD\) meet at \(O\). Through \(O\), draw \(PQ\parallel AB\) meeting \(AD\) at \(P\) and \(BC\) at \(Q\). Prove that \(PO=QO\).

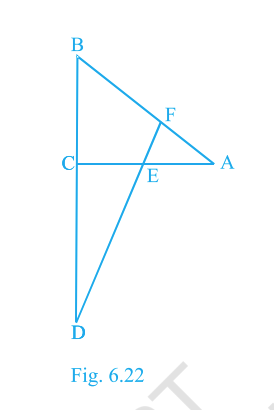
In Fig. 6.22, segment \(DF\) meets \(AC\) at \(E\) in \(\triangle ABC\), where \(E\) is the midpoint of \(CA\) and \(\angle AEF=\angle AFE\). Prove

\[\dfrac{BD}{CD}=\dfrac{BF}{CE}.\]

Prove that the area of the semicircle on the hypotenuse of a right triangle equals the sum of the areas of the semicircles on the other two sides.

Prove that the area of the equilateral triangle on the hypotenuse of a right triangle equals the sum of the areas of the equilateral triangles on the other two sides.