NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1Question 10
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1
Question. 10
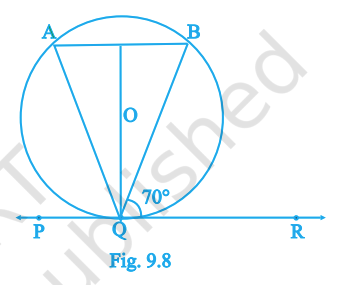
10. In Fig. 9.8, if \(PQR\) is the tangent at \(Q\) (centre \(O\)), \(AB\) is a chord parallel to \(PR\) and \(\angle BQR=70^\circ\), then \(\angle AQB\) equals
\(20^\circ\)
\(40^\circ\)
\(35^\circ\)
\(45^\circ\)
Detailed Answer with Explanation:
Step 1: We are given that \(PQR\) is a tangent at point \(Q\). The angle between tangent \(QR\) and chord \(QB\) is given as \(\angle BQR = 70^\circ\).
Step 2: By the Alternate Segment Theorem, the angle between a tangent and a chord is equal to the angle made by the chord in the opposite segment of the circle.
Step 3: So, \(\angle BQR = 70^\circ\) will be equal to the angle at point \(A\) on the other side of chord \(QB\). That means \(\angle QAB = 70^\circ\).
Step 4: Similarly, because chord \(AB\) is parallel to line \(PR\), we also get that \(\angle QBA = 70^\circ\).
Step 5: Now, in triangle \(AQB\): \[ \angle QAB + \angle QBA + \angle AQB = 180^\circ \]
Step 6: Substituting the values: \[ 70^\circ + 70^\circ + \angle AQB = 180^\circ \]
Step 7: Simplify: \[ 140^\circ + \angle AQB = 180^\circ \]
Step 8: Therefore, \[ \angle AQB = 180^\circ - 140^\circ = 40^\circ \]
Final Answer: \(\angle AQB = 40^\circ\). Hence, the correct option is B.