NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1Question 2
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1
Question. 2
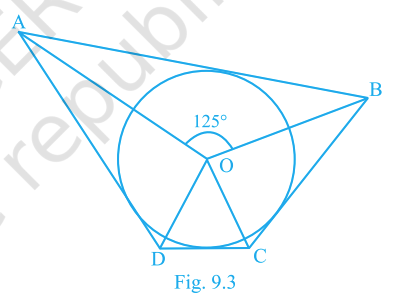
2. In Fig. 9.3, if \(\angle AOB = 125^\circ\), then \(\angle COD\) is equal to
(A)
\(62.5^\circ\)
(B)
\(45^\circ\)
(C)
\(35^\circ\)
(D)
\(55^\circ\)
Detailed Answer with Explanation:
Step 1: The figure shows a circle with centre O. The angles \(\angle AOB\) and \(\angle COD\) are central angles that lie on a straight line (diameter).
Step 2: Angles on a straight line always add up to \(180^\circ\). This is called the linear pair property.
Step 3: Here, \(\angle AOB + \angle COD = 180^\circ\).
Step 4: Substitute the given value: \(125^\circ + \angle COD = 180^\circ\).
Step 5: Subtract \(125^\circ\) from both sides: \(\angle COD = 180^\circ - 125^\circ = 55^\circ\).
Final Answer: \(\angle COD = 55^\circ\). So, the correct option is D.