NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4Question 10
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4
Question. 10
In Fig. 9.19, the common tangent, AB and CD to two circles with centres O and O′ intersect at E. Prove that the points O, E, O′ are collinear.
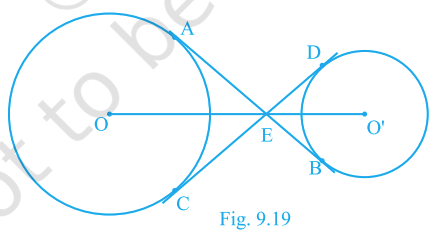
Answer:
O, E, O′ are collinear.
Detailed Answer with Explanation:
Step 1: Understand the problem.
We are given two circles. Their centres are O and O′. A common tangent AB and another common tangent CD meet at a point E.
Step 2: Recall the property of tangents.
The line drawn from an external point (E) to a circle touches the circle at only one point. The line joining the centre of the circle and the external point is always the angle bisector of the angle between the two tangents.
Step 3: Apply this property to the first circle with centre O.
From E, two tangents are drawn to this circle: EA and EC.
Therefore, the line joining O and E will bisect the angle ∠AEC.
Step 4: Apply the same property to the second circle with centre O′.
From E, two tangents are drawn to this circle: EB and ED.
Therefore, the line joining O′ and E will bisect the angle ∠BED.
Step 5: Notice the relation between ∠AEC and ∠BED.
Angles ∠AEC and ∠BED are supplementary (their sum is 180°), because AB and CD are straight lines meeting at E.
Step 6: Combine both results.
Since OE bisects ∠AEC and O′E bisects ∠BED, both OE and O′E lie along the same straight line that divides the straight angle (180°) at E into two equal halves.
Step 7: Conclusion.
Therefore, O, E, and O′ all lie on the same straight line. In other words, O, E, O′ are collinear.