NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4Question 11
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4
Question. 11
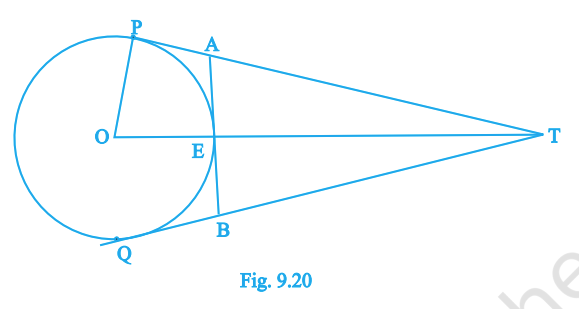
In Fig. 9.20, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.
Answer:
\(AB = 12\,\text{cm}\)
Detailed Answer with Explanation:
Step 1: We are given that:
- O is the centre of the circle.
- The radius of the circle is \(OE = 5\,\text{cm}\).
- The distance from O to point T is \(OT = 13\,\text{cm}\).
- AB is the tangent at point E, and tangents are always perpendicular to the radius at the point of contact.
Step 2: In right-angled triangle OEA:
- Hypotenuse = OT = \(13\,\text{cm}\)
- One side = OE (radius) = \(5\,\text{cm}\)
- The other side = AE (which is half of AB, since AB is symmetric).
Step 3: By Pythagoras’ theorem:
\[ OT^2 = OE^2 + AE^2 \]
Substituting the values:
\[ 13^2 = 5^2 + AE^2 \]
\[ 169 = 25 + AE^2 \]
Step 4: Simplify to find AE:
\[ AE^2 = 169 - 25 = 144 \]
\[ AE = \sqrt{144} = 12\,\text{cm} \]
Step 5: Since AB is tangent at E and passes through both sides of AE, the length of AB = AE = \(12\,\text{cm}\).
Final Answer: The length of the tangent AB is:
\[ AB = 12\,\text{cm} \]