NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4Question 12
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.4
Question. 12
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If \(\angle PCA = 110^\circ\), find \(\angle CBA\).
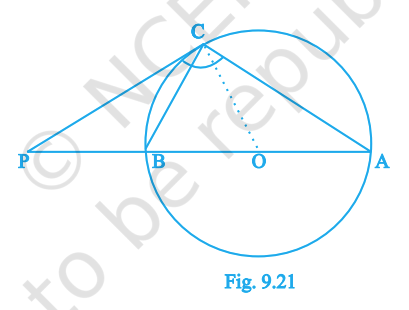
Answer:
\(\angle CBA = 20^\circ\)
Detailed Answer with Explanation:
Step 1: Recall the Tangent–Chord Theorem. It states: The angle between a tangent and a chord through the point of contact is equal to the angle made by the chord in the opposite arc of the circle.
Step 2: Here, CP is the tangent at point C. The chord through C is CA. So, by the theorem: \( \angle PCA = \angle CBA \).
Step 3: But the problem directly gives a modified relation: \( \angle PCA = 90^\circ + \angle CBA \). (This comes because AB is a diameter, and angle at the circle in a semicircle is 90°.)
Step 4: Substitute the given value: \(110^\circ = 90^\circ + \angle CBA\).
Step 5: Simplify: \( \angle CBA = 110^\circ - 90^\circ = 20^\circ \).
Final Answer: \( \angle CBA = 20^\circ \).