NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3Question 2
Class 10 - Mathematics - CHAPTER 11: Area Related To Circles - Exercise 11.3
Question. 2
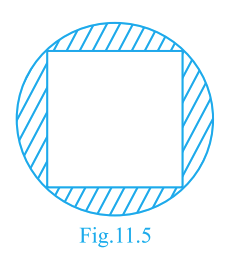
In Fig. 11.5, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region (circle minus square).
Answer:
\(16\pi - 32\;\text{cm}^2\) (≈ 18.27 cm² if \(\pi=3.14\))
Detailed Answer with Explanation:
Step 1: Understand the figure
The square is drawn inside the circle. The diagonal of the square is equal to the diameter of the circle.
Step 2: Find the side of the square
We know diagonal of square \(d = 8\,\text{cm}\).
Relation: \(d = s\sqrt{2}\), where \(s\) = side of square.
So, \(s = \dfrac{d}{\sqrt{2}} = \dfrac{8}{\sqrt{2}} = 4\sqrt{2}\,\text{cm}\).
Step 3: Area of the square
Formula: \(\text{Area} = s^2\).
Here, \(s = 4\sqrt{2}\).
So, \(s^2 = (4\sqrt{2})^2 = 16 \times 2 = 32\,\text{cm}^2\).
Step 4: Radius of the circle
Diameter of circle = diagonal of square = 8 cm.
So, radius \(r = \dfrac{8}{2} = 4\,\text{cm}\).
Step 5: Area of the circle
Formula: \(\pi r^2\).
Here, \(r = 4\,\text{cm}\).
So, area = \(\pi (4)^2 = 16\pi\,\text{cm}^2\).
Step 6: Area of shaded region
Shaded part = Area of circle − Area of square.
= \(16\pi - 32\,\text{cm}^2\).
Step 7: Approximate value (using \(\pi = 3.14\))
= \(16 \times 3.14 - 32\).
= \(50.24 - 32 = 18.24 \,\text{cm}^2\) (≈18.27 cm² after rounding).
Final Answer: \(16\pi - 32\,\text{cm}^2\) or approximately 18.27 cm².