NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.2Question 4
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.2
Question. 4
In Fig. 6.4, \(BD\) and \(CE\) intersect each other at \(P\). Is \(\triangle PBC \sim \triangle PDE\)? Why?
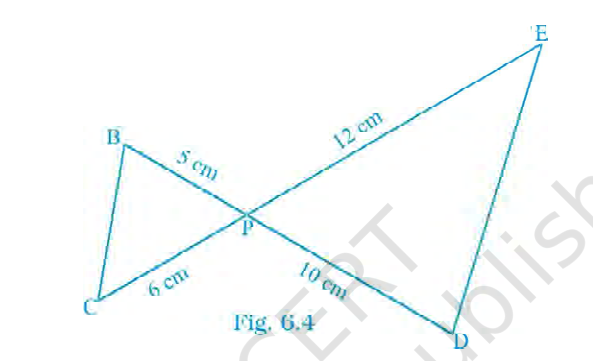
Answer:
Yes.
Video Explanation:
Detailed Answer with Explanation:
Step 1: Note the given lengths from the figure.
- \(PB = 5\,\text{cm}\)
- \(PC = 6\,\text{cm}\)
- \(PD = 10\,\text{cm}\)
- \(PE = 12\,\text{cm}\)
Step 2: Write the ratios of the sides of the two triangles.
For \(\triangle PBC\) and \(\triangle PDE\):
\[ \dfrac{PB}{PD} = \dfrac{5}{10} = \dfrac{1}{2}, \quad \dfrac{PC}{PE} = \dfrac{6}{12} = \dfrac{1}{2} \]
Step 3: Compare the included angle.
At point \(P\), the angle \(\angle BPC\) and the angle \(\angle DPE\) are equal because they are vertically opposite angles.
Step 4: Apply the SAS (Side–Angle–Side) similarity rule.
Since:
- Two pairs of sides are in the same ratio (\(\dfrac{1}{2}\)), and
- The included angle between those sides is equal,
Therefore, \(\triangle PBC \sim \triangle PDE\).