NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3
Question 5

Question. 5

In Fig. 6.10, if \(AB\parallel DC\) and lines \(AC\) and \(PQ\) meet at \(O\), prove that \(OA\cdot CQ = OC\cdot AP\).

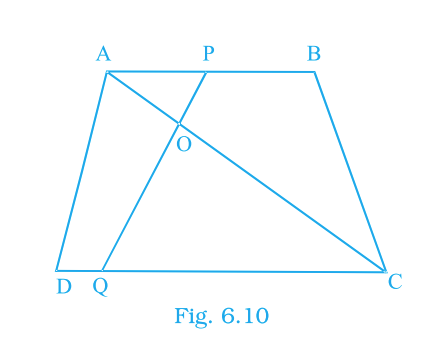
Fig. 6.10: Trapezium ABCD with AB ∥ DC, diagonal AC and a line PQ through A and D meeting BC at Q; AC and PQ intersect at O.

Answer:

Proved.

Detailed Answer with Explanation:

Step 1: We are given that \(AB \parallel DC\). Whenever two lines are parallel, we can use alternate interior angles property with a transversal.

Step 2: Consider the triangles \(\triangle AOP\) and \(\triangle COQ\).

  • Angle \(OAP = OCQ\) (because \(AB \parallel DC\), and \(PQ\) acts as a transversal → alternate interior angles are equal).
  • Angle \(AOP = COQ\) (they are vertically opposite angles at point \(O\)).

Step 3: Since two pairs of angles are equal, we can say that:

\(\triangle AOP \sim \triangle COQ\) (by AA similarity criterion).

Step 4: From similarity of triangles, the ratio of corresponding sides is equal:

\[ \dfrac{AO}{CO} = \dfrac{AP}{CQ} \]

Step 5: Now cross multiply:

\[ AO \cdot CQ = CO \cdot AP \]

Step 6: This is exactly what we had to prove.

Therefore, proved.

Open NCERT PDFOpen NCERT Answers PDF