NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 1
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 1
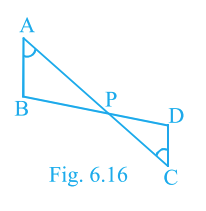
In Fig. 6.16, if \(\angle A = \angle C\), \(AB = 6\,\text{cm}\), \(BP = 15\,\text{cm}\), \(AP = 12\,\text{cm}\) and \(CP = 4\,\text{cm}\), find the lengths \(PD\) and \(CD\).
Answer:
\(PD = 5\,\text{cm},\; CD = 2\,\text{cm}.\)
Detailed Answer with Explanation:
Step 1: We are told that \(\angle A = \angle C\). Also, the angle at point \(P\) is common (vertically opposite). So, by AA similarity criterion, triangles \(\triangle APB\) and \(\triangle CPD\) are similar.
Step 2: For similar triangles, the ratios of their corresponding sides are equal. That means: \[ \dfrac{AB}{CD} = \dfrac{AP}{CP} = \dfrac{BP}{PD} \]
Step 3: Substitute the known values: - \(AB = 6\,\text{cm}\) - \(AP = 12\,\text{cm}\) - \(CP = 4\,\text{cm}\)
So, \[ \dfrac{AB}{CD} = \dfrac{AP}{CP} = \dfrac{12}{4} = 3 \]
Step 4: From this ratio, \[ \dfrac{AB}{CD} = 3 \quad \Rightarrow \quad CD = \dfrac{AB}{3} = \dfrac{6}{3} = 2\,\text{cm} \]
Step 5: Now use the ratio with \(BP\) and \(PD\): \[ \dfrac{BP}{PD} = 3 \]
So, \[ PD = \dfrac{BP}{3} = \dfrac{15}{3} = 5\,\text{cm} \]
Final Answer: \(PD = 5\,\text{cm}, \; CD = 2\,\text{cm}.\)