NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry - Exercise 7.4Question 5
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry - Exercise 7.4
Question. 5
Students stand on a grid for drill. Points \(A, B, C, D\) are shown below. Is it possible to place Jaspal so that he is equidistant from all four? If yes, give his position.
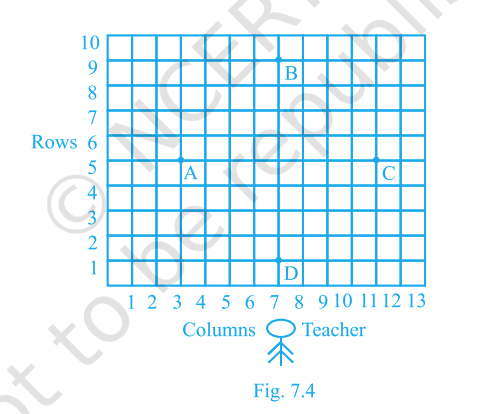
(Use grid coordinates: \(A(3,5),\ B(6,8),\ C(10,5),\ D(7,1)\).)
Answer:
Yes. Jaspal should stand at \(\bigl(6.5,\,4.5\bigr)\).
Detailed Answer with Explanation:
Step 1: To be equidistant from four points, Jaspal must stand at the circumcenter of the quadrilateral (if the four points lie on the same circle). The circumcenter is the point where the perpendicular bisectors of the sides meet.
Step 2: Take points \(A(3,5)\) and \(C(10,5)\). These two points are on the same horizontal line (since their \(y\)-coordinates are the same).
- The midpoint of \(AC\) is \(\bigl(\tfrac{3+10}{2},\tfrac{5+5}{2}\bigr)=(6.5,5)\).
- The line \(AC\) is horizontal, so its perpendicular bisector will be a vertical line.
- Equation of perpendicular bisector: \(x = 6.5\).
Step 3: Now consider \(B(6,8)\) and \(D(7,1)\).
- The midpoint of \(BD\) is \(\bigl(\tfrac{6+7}{2},\tfrac{8+1}{2}\bigr)=(6.5,4.5)\).
- Slope of \(BD\) = \(\tfrac{1-8}{7-6} = -7\).
- Slope of perpendicular bisector = negative reciprocal = \(-\tfrac{1}{-7}=\tfrac{1}{7}\).
- Equation of perpendicular bisector through midpoint: \(y-4.5=\tfrac{1}{7}(x-6.5)\).
Step 4: Find intersection of the two bisectors:
- From Step 2: \(x=6.5\).
- Substitute into equation of Step 3: \(y-4.5=\tfrac{1}{7}(6.5-6.5)=0\Rightarrow y=4.5\).
- So the intersection point is \((6.5,4.5)\).
Step 5: Check distances (all in SI units, each grid step is 1 unit):
- Distance to \(A(3,5)\): \(\sqrt{(6.5-3)^2+(4.5-5)^2}=\sqrt{(3.5)^2+(−0.5)^2}=\sqrt{12.25+0.25}=\sqrt{12.5}\).
- Distance to \(B(6,8)\): \(\sqrt{(6.5-6)^2+(4.5-8)^2}=\sqrt{0.25+12.25}=\sqrt{12.5}\).
- Distance to \(C(10,5)\): same calculation gives \(\sqrt{12.5}\).
- Distance to \(D(7,1)\): same calculation gives \(\sqrt{12.5}\).
Since all four distances are equal (about 3.54 units in SI), Jaspal can indeed be equidistant from all four points.
Final Answer: Jaspal should stand at position \(\boxed{(6.5,4.5)}\).