NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1Question 6
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1
Question. 6
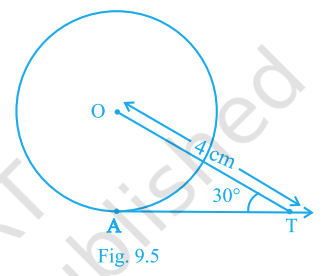
6. In Fig. 9.5, \(AT\) is a tangent to the circle with centre \(O\) such that \(OT=4\) cm and \(\angle OTA=30^\circ\). Then \(AT\) equals
4 cm
2 cm
\(2\sqrt{3}\) cm
\(4\sqrt{3}\) cm
Detailed Answer with Explanation:
Step 1: We are given that \(OT = 4\,\text{cm}\). Point \(T\) lies on the tangent \(AT\). So, \(OT\) is a line from the centre \(O\) to point \(T\).
Step 2: By the property of a tangent to a circle: the radius drawn to the point of tangency is perpendicular to the tangent. That means \(OA \perp AT\). So, triangle \(OTA\) is a right-angled triangle at \(A\).
Step 3: In right triangle \(OTA\), - Hypotenuse = \(OT = 4\,\text{cm}\). - Angle at \(T\) = \(30^\circ\).
Step 4: To find \(OA\) (radius), use the sine function: \[ \sin(30^\circ) = \dfrac{OA}{OT} \] Substituting values: \[ \sin(30^\circ) = \dfrac{OA}{4} \] \[ \dfrac{1}{2} = \dfrac{OA}{4} \] \[ OA = 2\,\text{cm} \]
Step 5: To find \(AT\) (the tangent), use the cosine function: \[ \cos(30^\circ) = \dfrac{AT}{OT} \] Substituting values: \[ \dfrac{\sqrt{3}}{2} = \dfrac{AT}{4} \] \[ AT = 4 \times \dfrac{\sqrt{3}}{2} \] \[ AT = 2\sqrt{3}\,\text{cm} \]
Final Answer: \(AT = 2\sqrt{3}\,\text{cm}\). (Option C)