NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1Question 7
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1
Question. 7
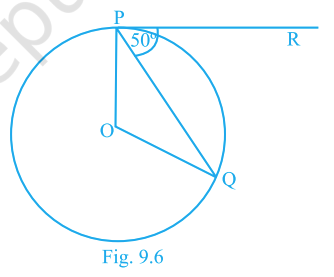
7. In Fig. 9.6, if \(O\) is the centre, \(PQ\) a chord and the tangent \(PR\) at \(P\) makes \(50^\circ\) with \(PQ\), then \(\angle POQ\) is
\(100^\circ\)
\(80^\circ\)
\(90^\circ\)
\(75^\circ\)
Detailed Answer with Explanation:
Step 1: Recall the Tangent–Chord Theorem: The angle between a tangent and a chord through the point of contact is equal to the angle made by the chord in the alternate segment of the circle.
Step 2: Here, tangent \(PR\) makes \(50^\circ\) with chord \(PQ\). So, \(\angle PQO = 50^\circ\) (angle in the alternate segment).
Step 3: In a circle, the central angle (angle at the centre) is always twice the angle at the circumference standing on the same chord.
Step 4: The chord is \(PQ\). Angle at the centre on chord \(PQ\) is \(\angle POQ\). Angle at the circumference is \(\angle PQO = 50^\circ\).
Step 5: Therefore, \[ \angle POQ = 2 \times \angle PQO = 2 \times 50^\circ = 100^\circ. \]
Final Answer: \(\angle POQ = 100^\circ\). Correct option: A