NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1Question 8
Class 10 - Mathematics - CHAPTER 9: Circles - Exercise 9.1
Question. 8
8. In Fig. 9.7, if \(PA\) and \(PB\) are tangents from \(P\) and \(\angle APB=50^\circ\), then \(\angle OAB\) equals
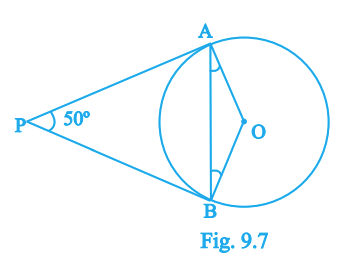
\(25^\circ\)
\(30^\circ\)
\(40^\circ\)
\(50^\circ\)
Detailed Answer with Explanation:
Step 1: The angle between two tangents drawn from a point outside the circle is related to the angle at the center. Formula: \( \angle APB + \angle AOB = 180^\circ \).
Step 2: We are given \( \angle APB = 50^\circ \). So, \( \angle AOB = 180^\circ - 50^\circ = 130^\circ \).
Step 3: Now look at triangle \(AOB\). Here, \(OA = OB\) because both are radii of the same circle. So, \( \triangle AOB \) is an isosceles triangle.
Step 4: In an isosceles triangle, the two base angles are equal. The sum of all angles in a triangle is \(180^\circ\). So, base angles = \( \dfrac{180^\circ - 130^\circ}{2} = \dfrac{50^\circ}{2} = 25^\circ \).
Step 5: That means \( \angle OAB = 25^\circ \).
Final Answer: Option A (\(25^\circ\)).