NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.1Question 1
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.1
Question. 1
1. In Fig. 6.2, \(\angle BAC = 90^\circ\) and \(AD \perp BC\). Then,
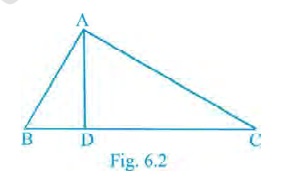
\(BD\cdot CD = BC^2\)
\(AB\cdot AC = BC^2\)
\(BD\cdot CD = AD^2\)
\(AB\cdot AC = AD^2\)
Detailed Answer with Explanation:
Step 1: The triangle \(ABC\) is a right triangle with \(\angle A = 90^\circ\). So, side \(BC\) is the hypotenuse.
Step 2: The line \(AD\) is drawn from the right angle \(A\) perpendicular to the hypotenuse \(BC\). This line is called the altitude on the hypotenuse.
Step 3: There is a special property of right triangles:
When an altitude is drawn from the right angle to the hypotenuse, the square of the altitude = product of the two parts of the hypotenuse.
In symbols: \(AD^2 = BD \times DC\).
Step 4: From the options, this matches option (C): \(BD \cdot CD = AD^2\).
Final Answer: Option (C).