NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.1Question 5
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.1
Question. 5
5. In Fig. 6.3, lines \(AC\) and \(BD\) intersect at \(P\). Given \(PA=6\,\text{cm},\; PB=3\,\text{cm},\; PC=2.5\,\text{cm},\; PD=5\,\text{cm},\; \(\angle APB=50^\circ\) and \(\angle CDP=30^\circ\). Find \(\angle PBA\).
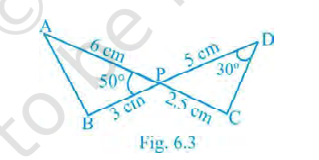
50°
30°
60°
100°
Detailed Answer with Explanation:
Step 1: Look at the lengths of the line segments.
We are given:
- \(PA = 6\,\text{cm}\)
- \(PB = 3\,\text{cm}\)
- \(PC = 2.5\,\text{cm}\)
- \(PD = 5\,\text{cm}\)
So, \(\dfrac{PA}{PB} = \dfrac{6}{3} = 2\).
And, \(\dfrac{PD}{PC} = \dfrac{5}{2.5} = 2\).
Step 2: Since the ratios are equal (both are 2), triangles \(\triangle APB\) and \(\triangle DPC\) are similar.
This means their angles are equal in pairs: \(\angle A = \angle D\), \(\angle B = \angle C\), etc.
Step 3: From the question, we know \(\angle CDP = 30^\circ\).
Because of similarity, \(\angle A = \angle D = 30^\circ\).
Step 4: In triangle \(APB\):
- \(\angle APB = 50^\circ\) (given)
- \(\angle PAB = 30^\circ\) (from similarity)
- \(\angle PBA = ?\)
Step 5: The sum of angles in any triangle is \(180^\circ\).
So,
\(\angle PBA = 180^\circ - (\angle APB + \angle PAB)\)
\(= 180^\circ - (50^\circ + 30^\circ)\)
\(= 180^\circ - 80^\circ\)
\(= 100^\circ\).
Final Answer: \(\angle PBA = 100^\circ\).