NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3Question 13
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3
Question. 13
In Fig. 6.12, if \(\angle ACB = \angle CDA\), \(AC=8\,\text{cm}\) and \(AD=3\,\text{cm}\), find \(BD\).
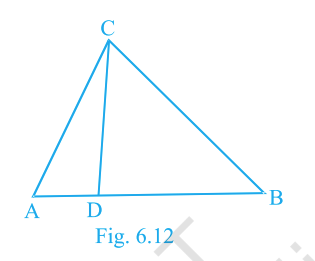
Answer:
\(\dfrac{55}{3}\,\text{cm}\)
Detailed Answer with Explanation:
Step 1: We are given that \(\angle ACB = \angle CDA\). This tells us that \(\triangle ACB\) and \(\triangle CDA\) are similar by AA similarity (two equal angles).
Step 2: From similarity of triangles, the sides are in proportion: \[ \dfrac{AC}{AD} = \dfrac{AB}{AC} \]
Step 3: Cross multiply to remove the fraction: \[ AB \cdot AD = AC^2 \]
Step 4: Substitute the given values: - \(AC = 8\,\text{cm}\) - \(AD = 3\,\text{cm}\) So, \[ AB \times 3 = 8^2 \] \[ AB \times 3 = 64 \]
Step 5: Divide both sides by 3 to get AB: \[ AB = \dfrac{64}{3}\,\text{cm} \]
Step 6: Now, \(BD = AB - AD\). Substitute values: \[ BD = \dfrac{64}{3} - 3 \] Convert 3 into fraction with denominator 3: \[ BD = \dfrac{64}{3} - \dfrac{9}{3} \]
Step 7: Simplify the fraction: \[ BD = \dfrac{55}{3}\,\text{cm} \]
Final Answer: \(BD = \dfrac{55}{3}\,\text{cm}\).