NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 10
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 10
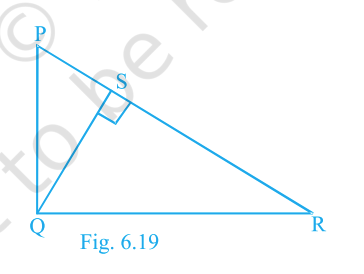
In Fig. 6.19, \(\triangle PQR\) is right-angled at \(Q\) and \(QS\perp PR\). If \(PQ=6\,\text{cm}\), \(PS=4\,\text{cm}\), find \(QS\), \(RS\) and \(QR\).
Answer:
\(QS=2\sqrt5\,\text{cm},\; RS=5\,\text{cm},\; QR=3\sqrt5\,\text{cm}.\)
Detailed Answer with Explanation:
Step 1: Recall the property of a right triangle with altitude drawn to the hypotenuse.
- Here, \(QS\) is perpendicular to hypotenuse \(PR\).
- The property says:
\(PQ^2 = PS \times PR\),
\(QR^2 = RS \times PR\),
\(QS^2 = PS \times RS\).
Step 2: Use \(PQ^2 = PS \times PR\) to find \(PR\).
\(PQ = 6\,\text{cm},\; PS = 4\,\text{cm}\).
\(PQ^2 = PS \times PR\)
\(6^2 = 4 \times PR\)
\(36 = 4PR\)
\(PR = 36/4 = 9\,\text{cm}\).
Step 3: Find \(RS\).
Total hypotenuse \(PR = 9\,\text{cm}\).
\(PS = 4\,\text{cm}\).
So, \(RS = PR - PS = 9 - 4 = 5\,\text{cm}\).
Step 4: Use \(QS^2 = PS \times RS\) to find \(QS\).
\(QS^2 = 4 \times 5 = 20\).
\(QS = \sqrt{20} = 2\sqrt{5}\,\text{cm}\).
Step 5: Use \(QR^2 = RS \times PR\) to find \(QR\).
\(QR^2 = 5 \times 9 = 45\).
\(QR = \sqrt{45} = 3\sqrt{5}\,\text{cm}\).
Final Answer:
\(QS = 2\sqrt{5}\,\text{cm},\; RS = 5\,\text{cm},\; QR = 3\sqrt{5}\,\text{cm}.\)