NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 9
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 9
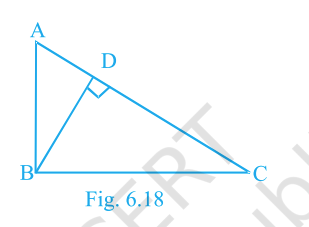
In Fig. 6.18, \(\triangle ABC\) is right-angled at \(B\) and \(BD\perp AC\). If \(AD=4\,\text{cm}\) and \(CD=5\,\text{cm}\), find \(BD\) and \(AB\).
Answer:
\(BD=2\sqrt{5}\,\text{cm},\; AB=6\,\text{cm}.\)
Detailed Answer with Explanation:
Step 1: First, add the two parts of \(AC\).
We are given: \(AD = 4\,\text{cm}\), \(CD = 5\,\text{cm}\).
So, \(AC = AD + CD = 4 + 5 = 9\,\text{cm}.\)
Step 2: Use the property of a right triangle with altitude drawn to the hypotenuse.
If \(BD\) is perpendicular to \(AC\), then: \(BD^2 = AD \times CD.\)
Substitute values: \(BD^2 = 4 \times 5 = 20.\)
So, \(BD = \sqrt{20} = 2\sqrt{5}\,\text{cm}.\)
Step 3: To find side \(AB\), use another property of the same theorem:
\(AB^2 = AD \times AC.\)
Substitute values: \(AB^2 = 4 \times 9 = 36.\)
So, \(AB = \sqrt{36} = 6\,\text{cm}.\)
Final Answer: \(BD = 2\sqrt{5}\,\text{cm}\) and \(AB = 6\,\text{cm}.\)