NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 13
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 13
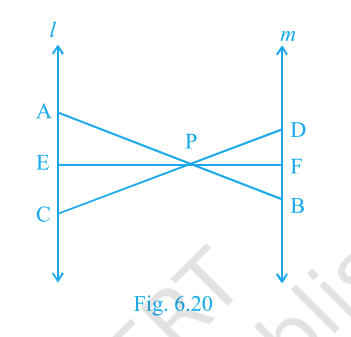
In Fig. 6.20, \(\ell\parallel m\) and the segments \(AB,\,CD,\,EF\) meet at \(P\). Prove
\[\dfrac{AE}{BF}=\dfrac{AC}{BD}=\dfrac{CE}{FD}.\]
Answer:
Proved.
Detailed Answer with Explanation:
Step 1: Notice that lines \(\ell\) and \(m\) are parallel, and point \(P\) is outside them. From \(P\), three lines \(AB, CD, EF\) are drawn cutting \(\ell\) at \(A, C, E\) and \(m\) at \(B, D, F\).
Step 2: Consider triangles \(\triangle PAE\) and \(\triangle PBF\).
- Both triangles have the common angle at \(P\).
- Also, \(\angle PAE = \angle PBF\) because \(\ell \parallel m\) (corresponding angles).
So, the two triangles are similar by AA (angle-angle) similarity.
Step 3: By similarity of \(\triangle PAE \sim \triangle PBF\): \[\dfrac{AE}{BF} = \dfrac{PE}{PF}.\]
Step 4: Next, consider triangles \(\triangle PAC\) and \(\triangle PBD\).
- Again, they share the common angle at \(P\).
- Also, \(\angle PAC = \angle PBD\) because \(\ell \parallel m\).
So, \(\triangle PAC \sim \triangle PBD\) (AA similarity).
Step 5: From this similarity, \[\dfrac{AC}{BD} = \dfrac{PC}{PD}.\]
Step 6: Similarly, consider triangles \(\triangle PCE\) and \(\triangle PDF\).
- They share angle at \(P\).
- Also, \(\angle PCE = \angle PDF\) because of parallel lines.
So, \(\triangle PCE \sim \triangle PDF\).
Step 7: From this similarity, \[\dfrac{CE}{FD} = \dfrac{PC}{PD}.\]
Step 8: Now, observe:
- From Step 3: \(\dfrac{AE}{BF} = \dfrac{PE}{PF}\).
- From Step 5: \(\dfrac{AC}{BD} = \dfrac{PC}{PD}\).
- From Step 7: \(\dfrac{CE}{FD} = \dfrac{PC}{PD}\).
Also, note that \(\dfrac{PE}{PF} = \dfrac{PC}{PD}\) since all come from similar triangles with vertex \(P\).
Final Step: Therefore, \[\dfrac{AE}{BF} = \dfrac{AC}{BD} = \dfrac{CE}{FD}.\]
Hence proved.