NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 14
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 14
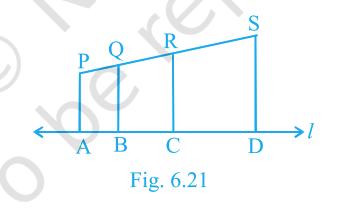
In Fig. 6.21, \(PA, QB, RC, SD\) are all perpendicular to a line \(\ell\). Given \(AB=6\,\text{cm}\), \(BC=9\,\text{cm}\), \(CD=12\,\text{cm}\) and \(SP=36\,\text{cm}\). Find \(PQ, QR, RS\).
Answer:
\(PQ=4\,\text{cm},\; QR=4\,\text{cm},\; RS=20\,\text{cm}.\)
Detailed Answer with Explanation:
Step 1: Observe the figure. The line \(\ell\) is horizontal, and the perpendiculars \(PA, QB, RC, SD\) are vertical heights.
Step 2: Notice that triangles formed (like \(\triangle PAB, \triangle QBC, \triangle RCD, \triangle S(AB+BC+CD)\)) are similar because they all have the same angle at the base and a right angle.
👉 This means heights are proportional to the base lengths on line \(\ell\).
Step 3: Let the constant of proportionality be \(k\). Then: \[ PA = k \times AB, \quad QB = k \times BC, \quad RC = k \times CD, \quad SD = k \times (AB+BC+CD) \]
Step 4: Calculate total base: \[ AB + BC + CD = 6 + 9 + 12 = 27\,\text{cm}. \]
Step 5: We are given \(SD = 36\,\text{cm}\). So, \[ 36 = k \times 27 \quad \Rightarrow \quad k = \dfrac{36}{27} = \dfrac{4}{3}. \]
Step 6: Now find each perpendicular length: \[ PA = k \times 6 = \dfrac{4}{3} \times 6 = 8\,\text{cm}, QB = k \times 9 = \dfrac{4}{3} \times 9 = 12\,\text{cm}, RC = k \times 12 = \dfrac{4}{3} \times 12 = 16\,\text{cm}, SD = 36\,\text{cm (already given)}. \]
Step 7: Use differences to find the required distances:
- \(PQ = QB - PA = 12 - 8 = 4\,\text{cm}\)
- \(QR = RC - QB = 16 - 12 = 4\,\text{cm}\)
- \(RS = SD - RC = 36 - 16 = 20\,\text{cm}\)
Final Answer: \(PQ = 4\,\text{cm},\; QR = 4\,\text{cm},\; RS = 20\,\text{cm}.\)