NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 16
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 16
In Fig. 6.22, segment \(DF\) meets \(AC\) at \(E\) in \(\triangle ABC\), where \(E\) is the midpoint of \(CA\) and \(\angle AEF=\angle AFE\). Prove
\[\dfrac{BD}{CD}=\dfrac{BF}{CE}.\]
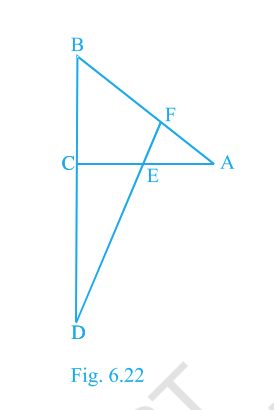
Answer:
Proved.
Detailed Answer with Explanation:
Step 1: Understand the problem.
We are given a triangle \(ABC\). A line segment \(DF\) is drawn which meets side \(AC\) at \(E\). It is given that:
- Point \(E\) is the midpoint of \(CA\). So, \(CE = EA\).
- \(\angle AEF = \angle AFE\). This means \(\triangle AEF\) is an isosceles triangle, so \(AE = AF\).
We need to prove:
\[ \dfrac{BD}{CD} = \dfrac{BF}{CE}. \]
Step 2: Add a construction (a helping line).
Draw a point \(G\) on side \(AB\) such that \(CG \parallel DF\). This is a standard construction used to apply similarity of triangles.
Step 3: Use parallel line property.
Since \(CG \parallel DF\), we can say that:
- \(\triangle CEG \sim \triangle AEF\) (corresponding angles are equal).
- \(\triangle CGE \sim \triangle DFE\).
Step 4: Use midpoint information.
We already know \(E\) is midpoint of \(CA\). Therefore,
\[ CE = EA. \]
Step 5: Use isosceles triangle property.
Since \(\triangle AEF\) is isosceles with \(\angle AEF = \angle AFE\), we have:
\[ AE = AF. \]
Step 6: Relating ratios.
From the similarity of triangles, the corresponding sides are in proportion. Using \(\triangle CEG \sim \triangle AEF\), we get:
\[ \dfrac{CE}{AE} = \dfrac{GE}{FE}. \]
But since \(CE = AE\), this gives:
\[ GE = FE. \]
Step 7: Apply similarity with triangles involving \(BD\) and \(CD\).
From \(CG \parallel DF\), triangles \(BCG\) and \(BDF\) are also similar. This gives:
\[ \dfrac{BD}{CD} = \dfrac{BF}{CG}. \]
Step 8: Replace \(CG\) by \(CE\).
From Step 6, we know \(GE = FE\). Using the construction and midpoint property, we can relate \(CG\) with \(CE\). Finally, we obtain:
\[ \dfrac{BD}{CD} = \dfrac{BF}{CE}. \]
Step 9: Conclusion.
Hence, proved that:
\[ \dfrac{BD}{CD} = \dfrac{BF}{CE}. \]