NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4Question 4
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.4
Question. 4
In Fig. 6.17, \(PQRS\) is a parallelogram and \(AB\parallel PS\). Prove that \(OC\parallel SR\).
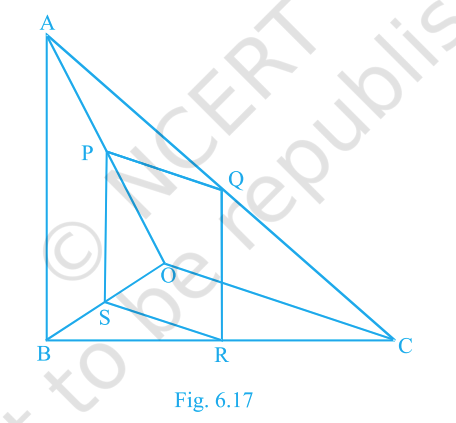
Answer:
Proved.
Detailed Answer with Explanation:
Step 1: We are given that \(PQRS\) is a parallelogram. So, opposite sides are parallel. That means \(PQ \parallel SR\) and \(PS \parallel QR\).
Step 2: It is also given that \(AB \parallel PS\). Since \(PS \parallel QR\), we can say: \(AB \parallel QR\).
Step 3: Look at diagonal \(PR\). It cuts the parallelogram into two triangles: - \(\triangle APS\) on the left, - \(\triangle PQR\) on the right.
Step 4: In \(\triangle PQR\), line \(AB\) is drawn parallel to \(QR\). From the Basic Proportionality Theorem (Thales’ theorem), we know this will divide the sides proportionally.
Step 5: By that property, we can say the triangles formed are similar: \(\triangle OAB \sim \triangle OPS\) (AA similarity, because corresponding angles are equal when lines are parallel).
Step 6: From similarity, corresponding sides are parallel. That gives \(OC \parallel SR\).
Step 7: Therefore, we have proved that \(OC \parallel SR\).
Final Answer: \(OC \parallel SR\).