NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3Question 2
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3
Question. 2
Find the value of \(x\) for which \(DE \parallel AB\) in Fig. 6.8.
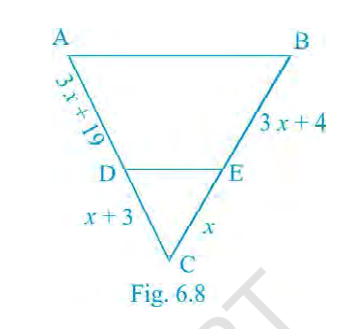
Answer:
\(x=2\)
Detailed Answer with Explanation:
Step 1: Since \(DE \parallel AB\), the line \(DE\) divides the sides of triangle \(\triangle CBA\) in the same ratio. So, \(\triangle CDE \sim \triangle CBA\) (corresponding angles are equal).
Step 2: From similarity, we know: \[ \dfrac{CD}{CA} = \dfrac{CE}{CB} \]
Step 3: Write the lengths of the sides using the given values: - On side \(CA\): \(AD = 3x+19\) and \(DC = x+3\). So total \(CA = AD + DC = (3x+19) + (x+3) = 4x+22\). And \(CD = x+3\).
- On side \(CB\): \(BE = 3x+4\) and \(EC = x\). So total \(CB = BE + EC = (3x+4) + x = 4x+4\). And \(CE = x\).
Step 4: Put the values into the ratio: \[ \dfrac{CD}{CA} = \dfrac{CE}{CB} \] \[ \dfrac{x+3}{4x+22} = \dfrac{x}{4x+4} \]
Step 5: Cross multiply to remove the fractions: \[ (x+3)(4x+4) = x(4x+22) \]
Step 6: Expand both sides: Left side: \( (x+3)(4x+4) = 4x^2 + 4x + 12x + 12 = 4x^2 + 16x + 12 \). Right side: \( x(4x+22) = 4x^2 + 22x \).
Step 7: Equating both sides: \[ 4x^2 + 16x + 12 = 4x^2 + 22x \]
Step 8: Cancel \(4x^2\) from both sides: \[ 16x + 12 = 22x \]
Step 9: Rearrange: \[ 12 = 22x - 16x = 6x \]
Step 10: Divide both sides by 6: \[ x = 2 \]
Final Answer: \(x=2\).