NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3
Question 3

Question. 3

In Fig. 6.9, if \(\angle 1=\angle 2\) and \(\triangle NSQ \cong \triangle MTR\), prove that \(\triangle PTS \sim \triangle PRQ\).

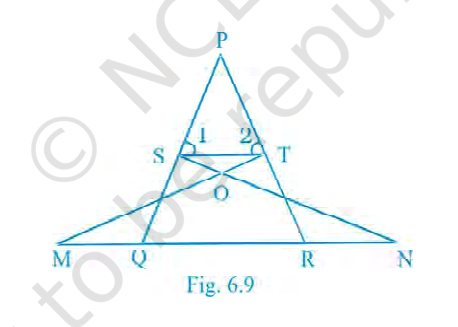
Fig. 6.9: Large triangle PNR with base MQRN, cevians through S and T to Q and R.

Answer:

Proved.

Detailed Answer with Explanation:

Step 1: It is given that \(\triangle NSQ \cong \triangle MTR\).

From congruence, we know that corresponding angles and sides are equal. So, \(\angle SQN = \angle TRM\) and \(SQ = TR\).

Step 2: Points \(M, Q, R, N\) are collinear (they lie on a straight line). Using this and the equal angles \(\angle SQN = \angle TRM\), we can say that line segment \(QS \parallel RT\).

Step 3: It is also given that \(\angle 1 = \angle 2\). These are the angles at point \(P\), so we can write: \(\angle SPT = \angle QPR\).

Step 4: Because \(QS \parallel RT\):

  • \(\angle PST = \angle PRQ\) (alternate interior angles)
  • \(\angle PTS = \angle PQR\) (corresponding angles)

Step 5: Now compare triangles \(PTS\) and \(PRQ\):

  • \(\angle SPT = \angle QPR\)
  • \(\angle PST = \angle PRQ\)

So, two pairs of corresponding angles are equal.

Step 6: By the AA similarity criterion, if two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.

Therefore, \(\triangle PTS \sim \triangle PRQ\).

Open NCERT PDFOpen NCERT Answers PDF