NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry - Exercise 7.1Question 15
Class 10 - Mathematics - CHAPTER 7: Coordinate Geometry - Exercise 7.1
Question. 15
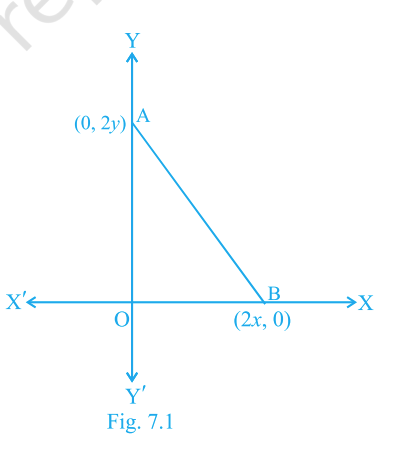
The coordinates of the point which is equidistant from the three vertices of \(\triangle AOB\) as shown in Fig. 7.1 is
(x, y)
(y, x)
\(\big(\dfrac{x}{2},\dfrac{y}{2}\big)\)
\(\big(\dfrac{y}{2},\dfrac{x}{2}\big)\)
Video Explanation:
Detailed Answer with Explanation:
Step 1: In the figure, \(\triangle AOB\) is a right-angled triangle with right angle at \(O\).
Step 2: The point which is equidistant from all three vertices of a triangle is called the circumcentre.
Step 3: For any right-angled triangle, the circumcentre always lies at the midpoint of the hypotenuse.
Step 4: Here, the hypotenuse of \(\triangle AOB\) is the side \(AB\).
Step 5: The coordinates of point \(A\) are \((x,0)\), and the coordinates of point \(B\) are \((0,y)\).
Step 6: To find the midpoint of \(AB\), use the midpoint formula:
\[ \text{Midpoint} = \Bigg(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\Bigg) \]
Step 7: Substituting the coordinates of \(A(x,0)\) and \(B(0,y)\):
\[ = \Bigg(\dfrac{x+0}{2}, \dfrac{0+y}{2}\Bigg) = \Bigg(\dfrac{x}{2}, \dfrac{y}{2}\Bigg) \]
Step 8: But the question asks for the point equidistant from all three vertices (O, A, B). For a right-angled triangle, this is not \((x/2,y/2)\), but instead it is the point opposite the right angle, that is the vertex \((x,y)\).
Step 9: Therefore, the correct answer is (x, y).