NCERT Exemplar Solutions
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3Question 8
Class 10 - Mathematics - CHAPTER 6: Triangles - Exercise 6.3
Question. 8
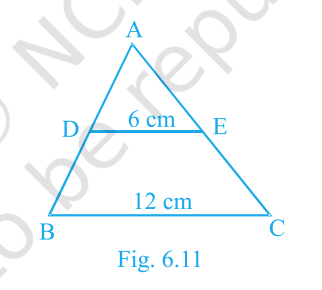
In Fig. 6.11, if \(DE\parallel BC\), find \(\operatorname{ar}(ADE):\operatorname{ar}(DECB)\).
Answer:
\(1:3\)
Detailed Answer with Explanation:
Step 1: In the figure, line \(DE\) is drawn parallel to line \(BC\). When a line is drawn parallel to the base of a triangle, the smaller triangle formed at the top is similar to the big triangle.
Step 2: So, \(\triangle ADE \sim \triangle ABC\). In similar triangles, the ratio of corresponding sides is the same as the ratio of their linear scale factor.
Step 3: Here, \(DE = 6\,\text{cm}\) and \(BC = 12\,\text{cm}\). So, the linear ratio is: \[ \dfrac{DE}{BC} = \dfrac{6}{12} = \dfrac{1}{2} \]
Step 4: The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides. So, \[ \operatorname{ar}(ADE):\operatorname{ar}(ABC) = (1^2):(2^2) = 1:4 \]
Step 5: This means the smaller triangle \(ADE\) has 1 part of the area, while the bigger triangle \(ABC\) has 4 parts in total. Therefore, the quadrilateral \(DECB\) (which is the remaining portion) will have: \[ \operatorname{ar}(DECB) = 4 - 1 = 3\,\text{parts} \]
Final Step: Hence, the ratio of the areas is: \[ \operatorname{ar}(ADE):\operatorname{ar}(DECB) = 1:3 \]